Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 19.1 - Ex. 45
Uma máquina de Carnot trabalha entre dois reservatórios de calor como um refrigerador. Durante cada ciclo, de calor são absorvidos do reservatório frio e de calor são liberados para o reservatório quente. (a) Qual é o rendimento da máquina de Carnot, quando ela trabalha como uma máquina térmica entre os mesmos dois reservatórios? (b) Mostre que nenhuma outra máquina, trabalhando como um refrigerador entre os mesmo dois reservatórios, pode ter um CD maior do que .
Passo 1
a) Para calcular a eficiência do ciclo de Carnot a gente só precisa usar a fórmulinha:
Como a gente tem um refrigerador, é o trabalho que entra no sistema e é calor que vai para o reservatório quente, que ele diz ser .
Falta a gente achar . Olha o esqueminha do refrigerador:
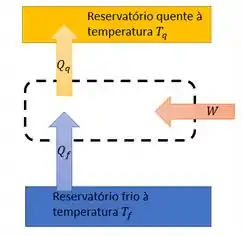
O que entra no sistema do refrigerador é o trabalho e calor que sai do reservatório frio. E o que sai do sistema é o calor que vai para o reservatório quente. Então, podemos escrever isso numa expressãozinha:
Daí a gente pode tirar o trabalho para usar na fórmulinha do rendimento, porque o enunciado diz que
Substituindo isso na fórmula do rendimento:
Passo 2
b) O coeficiente de desempenho (CD) do refrigerador é dado pela expressão
Ele fala para a gente provar que esse não pode ser maior 2. E ele fala para considerarmos os mesmos reservatórios, então
Vamos fazer um teste: vamos usar nosso , e na fórmula do :
Então para nosso refrigerador funcionar exatamente como no item a) ele precisa ter CD igual a 2, e todos esses valores de troca de calor e trabalho.
Passo 3
Mas qual é o problema se CD for maior, mas as condições de calor trocado não mudarem?
Olha para a expressão de novo
E lembra da expressão que a gente viu no passo 1
Quanto maior for o CD, menor é o trabalho segundo a equação . Então para temos .
Só que se o trabalho diminuir para um valor menor que e o calor retirado da fonte fria continuar , pela equação , o calor que vai para a fonte quente diminui, então vai deixar de bater com , vai ser menor.
O único jeito de continuar em , mesmo quando , seria se a quantidade de calor que falta para chegar em saísse do reservatório frio para o quente sem precisar absorver trabalho, mas isso é impossível!
Porque a única transferência de calor que não absorve trabalho é de um reservatório quente para o frio. Logo, é impossível que .