Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 5.Problemas - Ex. 75
Uma máquina de lavar em aço está suspensa no interior de um engradado, a partir de um fio leve que está preso ao topo do engradado. Este desliza para baixo de uma longa rampa com
inclinação que forma um ângulo de acima do plano horizontal. A massa do engradado é de 180 kg. Você está sentado dentro do engradado (com uma lanterna); a sua massa é de 55 kg. À
medida que o engradado desliza rampa abaixo, você nota que a lavadora fica em repouso em relação ao engradado quando o fio forma um ângulo de com o topo do engradado. Qual é o coeficiente de atrito cinético entre a rampa e o engradado?
Passo 1
Como a arruela está em repouso em relação à caixa, esses dois objetos têm a mesma aceleração.
Vamos esboçar o diagrama de corpo livre da arruela:
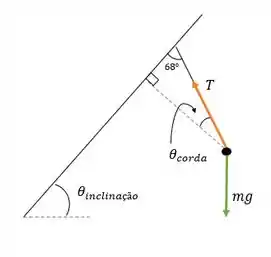
Passo 2
Vamos observar o ângulo da corda medido da perpendicular à parte superior da caixa.
Esse ângulo é:
Passo 3
O diagrama de corpo livre para a arruela nos leva às seguintes equações, usando a Segunda Lei de Newton e tomando a direção ascendente como positiva:
1ª equação:
2ª equação:
Dividindo as duas equações, ficamos com:
Passo 4
Para a caixa, o componente do peso ao longo da inclinação é:
E a força normal é:
Então, usando a segunda lei de Newton novamente:
Passo 5
Isso nos leva a seguinte observação: de que a corda ficará pendurada em um ângulo cuja tangente é igual ao coeficiente de atrito cinético: