Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 5.Problemas - Ex. 68
Um lavador de vidraças empurra sua escova com velocidade constante para cima de uma janela vertical aplicando uma força , como indicado na Figura 5.65. A escova pesa 12,0 N e o coeficiente de atrito cinético é . Ache a) o módulo da força ; b) a força normal
exercida pela janela sobre a escova.
Passo 1
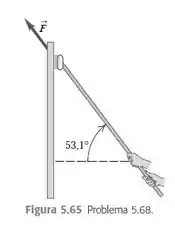
Eaee, belezinha?? Bom... o enunciado nos diz que um lavador de vidraças empurra sua escova com velocidade constante para cima de uma janela vertical aplicando uma força , como indicado na figura abaixo:
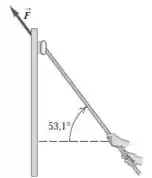
. A escova pesa e o coeficiente de atrito cinético é .
Queremos encontrar o módulo de e a força normal exercida pela janela sobre a escova.
Para resolver isso, temos que fazer um diagrama de corpo livre do sistema e analisar as forças que estão atuando no corpo.
Também, utilizaremos também a segunda Lei de Newton:
Onde é a força resultante, é a massa e é a aceleração.
Passo 2
Bom... Velocidade constante significa que a aceleração é nula.
Observe que a força normal exercida pela parede é horizontal, pois é perpendicular à parede.
A força cinética de atrito exercida pela parede é paralela à parede e se opõe ao movimento, sendo verticalmente para baixo.
Então, vamos desenhar o diagrama de corpo livre dessa caso:
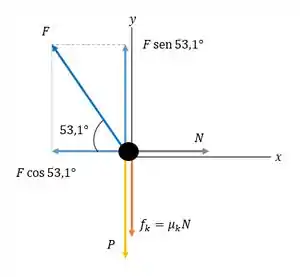
Passo 3
E então vamos aplicar a segunda lei de Newton no pincel.
No :
A força de atrito é:
Onde é o coeficiente de atrito e é a força normal.
Passo 4
No :
Onde é a força peso.
Passo 5
- Dessa forma temos que é:
- E assim, a normal é dada por: