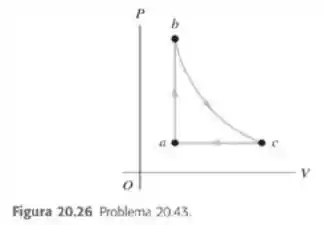
Uma máquina térmica funciona seguindo o ciclo mostrado na Figura 20.26. A substância de trabalho é de gás hélio, que atinge uma temperatura máxima de . considere o hélio um gas ideal. O processo é isotérmico. A pressão nos estados e é , e apressão no estado é . a) Quanto trabalho a máquina realiza a cada ciclo, e qual sua eficiência? c) Compare a eficiência dessa máquina com a máxima eficiência possível dos reservatórios quente e frio usados nesse ciclo.

Para o processo , que é isotérmico, podemos usar a equação:

O problema é que não temos o volume do ponto e nem do ponto , vamos usar a equação de gases ideais para encontrarmos :

Com os valores:

E então usamos de novo a equação, mas agora para igualar os valores dos dois pontos para encontrarmos :

A pressão de é a mesma que a de pelo gráfico e a pressão de é dada no enunciado, assim:

Substituindo tudo pelos valores que temos:

Substituindo todos os valores na equação para o calor:

E o calor do último processo , que está a pressão constante pode ser calculado por:

Substituindo os valores e as temperaturas que já temos dos dois pontos:

Como o último processo ocorre uma compressão, o calor que calculamos é liberado pelo gás. E nos outros dois processo o calor é absorvido, já que o processo é uma expansão e o processo a pressão sobe. Assim:

b) O trabalho do processo todo pode ser calculado através da primeira lei da termodinâmica, já que é um ciclo fechado, e:

E somando o calor total:

A eficiência será a razão entre o trabalho que acabamos de calcular e o calor absorvido pela máquina:

c) A máxima eficiência seria a eficiência de um ciclo de Carnot que utiliza as temperaturas dos reservatórios quente e frio:

A eficiência seria maior que o dobro para os mesmos reservatórios.