Enunciado
Física - Young and Freedman - Vol 2- Ed: 12º - Capítulo 12.Problemas desafioadores - Ex. 87
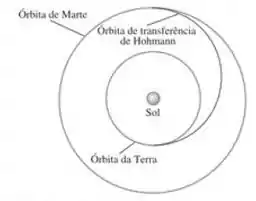
O método mais eficiente para enviar uma espaçonave da Terra a outro planeta consiste em usar uma órbita de transferência de Hohmann (figura 12.38). Se a órbita da partida e a órbita do destino forem circulares, a órbita de transferência de Hohmann será uma elipse cujo periélio tangencia a órbita de um dos planetas e cujo afélio tangencia a órbita do outro planeta. Os foguetes são acionados brevemente na órbita de partida para colocar a espaçonave na órbita de transferência; a seguir, a espaçonave viaja até atingir o planeta desejado. Depois, os foguetes são novamente acionados para colocar a espaçonave na mesma órbita em torno do Sol descrita pelo planeta do destino.
- Para uma viagem da Terra até Marte, qual deve ser a direção e o sentido em que o foguete deve ser disparado na Terra e em Marte: no sentido do movimento ou no sentido oposto ao do movimento? E no caso de uma viagem de Marte até a Terra?
- Quanto tempo entre os disparos dos foguetes levaria uma viagem de ida da Terra até Marte?
- Para atingir Marte a partir da Terra, o lançamento deve ser cronometrado de modo que Marte deve estar no local exato de sua órbita quando a trajetória da espaçonave tangencia a órbita do planeta em torno do Sol. Qual deve ser o ângulo entre a direção do lançamento e a direção da linha que une o Sol com Marte e da linha que une o Sol com a Terra? Use dados do Apêndice F.
Passo 1
Olá, tudo bem? Essa questão parece complicada, mas vou ajudar você aqui! Bora lá?
Letra a)
Para ir da órbita circular da Terra até a órbita de transferência, a energia da espaçonave deve aumentar certo? E os foguetes são disparados na direção oposta à do movimento, ou seja, na direção que aumenta a velocidade!
Uma vez na órbita de Marte, a energia precisa ser aumentada novamente e, portanto, os foguetes precisam ser disparados na direção oposta à do movimento. Na Figura do livro, o semi-eixo maior da órbita de transferência é a média aritmética dos raios da órbita da Terra e Marte e, portanto, a energia da espaçonave enquanto na órbita de transferência tem um valor entre as energias das órbitas circulares.
Retornando de Marte para a Terra, o procedimento é revertido e os foguetes são disparados contra a direção do movimento.
Então nos dois casos, o foguete deve ser disparado no sentido contrário ao do movimento!
Passo 2
Letra b)
Vamos primeiro relembrar da terceira lei de Kepler, certo? Ela nos diz que o período de rotação tem a ver com o semi-eixo maior da seguinte forma:
Beleza?
O tempo que queremos vai ser a metade desse período aí, pois só queremos o tempo de ida, ok?
E o semi-eixo? Bom, como falei ali em cima, ele vai ser a média aritmética dos raios da órbita da Terra e Marte:
Agora é só substituir na fórmula do período (e dividir por dois!) e achamos o tempo:
Passo 3
Letra c)
Do apêndice tiramos que Marte leva dias para uma volta completa, ou seja, para fazer . Sabemos que em um dia temos , então vamos fazer uma regrinha de três para saber o ângulo em :
A espaçonave passa por ele fazendo um ângulo de , então o ângulo entre eles é a diferença entre os ângulos: