Enunciado
Física - Young and Freedman - Vol 2- Ed: 12º - Capítulo 20.Problemas - Ex. 40
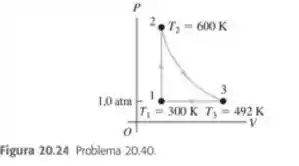
Uma máquina térmica usa de um gas diatômico ideal e executa o ciclo indicado no diagrama PV da figura 20.24. O processo ocorre a volume constante, o processo é adiabático e o processo ocorre a uma pressão constante de . O valor de para esse gás é . a) Ache a pressão e o volume nos pontos 1,2 e 3. b) Calcule , e em cada um dos três processos. c) Ache o trabalho total realizado pelo gás no ciclo. d) Calcule o fluxo de calor total para o interior da máquina em um ciclo. e) Qual é a eficiência térmica da máquina? Como esse valor se compara à eficiência do ciclo de Carnot operando entre as mesmas temperaturas extremas e ?
Passo 1
a) Para o processo , vamos usar a equação dos gases ideais para calcularmos a pressão do ponto 2:
Substituindo os valores:
E para calcularmos volume dos dois estados basta usarmos um dos valores de pressão na equação dos gases ideias e os valores dados de temperatura e número de moles:
Passo 2
Vamos usar o processo para calcularmos o volume e a pressão do ponto 3, como a pressão é constante, vamos usar a equação dos gases ideias mais uma vez e isolar a temperatura e o volume:
Como a gente já calculou o volume do estado 1, basta isolar e substituir os valores:
E como o processo ocorre a pressão constante, já temos o valor da pressão do ponto
Passo 3
b) Como o processo ocorre a volume constante, . E o calor pode ser calculado por:
Substituindo os valores e usando :
E pela primeira lei da termodinâmica:
Para o processo , , pois o processo é adiabático, podemos calcular a variação da energia interna pela equação:
Que pode ser usada para qualquer processo.
Substituindo os valores:
E a primeira lei da termodinâmica fica:
E para o processo , a pressão constante, podemos calcular o trabalho usando a equação:
Usando os valores que calculamos antes para os volumes e a pressão:
Para o calor podemos usar o e a equação que relaciona ele com a variação de temperatura:
E como
A equação fica:
Substituindo os valores:
Usando a primeira lei da termodinâmica para calcular a variação de energia interna:
Passo 4
c) O trabalho total será a soma dos trabalhos realizados em cada processo:
Passo 5
d) O calor utilizado pela máquina no ciclo é a soma do calor de cada processo, assim como fizemos com o trabalho:
Passo 6
e) A eficiência da máquina é dada pela razão entre o trabalho gerado e o calor absorvido pela máquina, que será o calor do processo :
Comparando essa eficiência com a eficiência de uma máquina de Carnot que usa as temperaturas extremas como o enunciado fala:
Que será quase cinco vezes maior.