Uma massa desliza de cima para baixo por um plano ligeiramente inclinado a partir de uma altura vertical , formando um ângulo com a horizontal.
a) O trabalho realizado por uma força é a soma do trabalho realizado pelos componentes da força. Considere os componentes da gravidade paralela e perpendicular à superfície do plano. Calcule o trabalho realizado sobre a massa por cada um dos componentes e use esses resultados para mostrar que o trabalho realizado pela gravidade é exatamente o
mesmo, caso a massa tivesse caído diretamente de cima para baixo pelo ar, de uma altura .
b) Use o teorema do trabalho energia para provar que a velocidade escalar da massa na base da inclinação seria a mesma, caso tivesse sido solta da altura , independentemente do ângulo da inclinação. Explique como essa velocidade escalar pode ser independente do ângulo da inclinação.
c) Use os resultados do item (b) para determinar a velocidade escalar de uma rocha que desliza de cima para baixo por uma colina coberta de gelo e sem atrito, partindo do repouso de um ponto que está acima da base.
Passo 1
Opa, bora resolver esse problema! Temos um objeto de massa deslizando em um plano inclinado da seguinte forma:
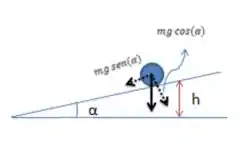
O trabalho em relação à componente paralela ao plano vai ser calculado usando a componente da força peso. E o deslocamento, em termos de e é , daí o trabalho paralelo vai ser:
O trabalho perpendicular vai ser dado usando a componente perpendicular da força . E quanto ao deslocamento? Bom, ele é zero nesse caso! Porque a bola desliza sobre o plano inclinado e não tem deslocamento na vertical. O trabalho perpendicular então é zero . O trabalho total vai ser a soma:
Então mostramos que o trabalho realizado pela gravidade é exatamente o mesmo, caso a massa tivesse caído diretamente de cima para baixo pelo ar, de uma altura .
Passo 2
Agora a gente tem que provar que a velocidade final do objeto independe do ângulo usando o teorema do trabalho energia.
Usando o teorema:
E considerando que a massa foi solta do topo do plano, a energia cinética inicial é zero. Reescrevendo a energia cinética final em termos da velocidade temos uma relação entre ela e a altura inicial:
E essa é a velocidade que encontramos com as equações de movimento e não depende do ângulo de inclinação, apenas da altura vertical inicial.
Passo 3
Usando a expressão pra velocidade e com vamos determinar a velocidade: