Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 2.Problemas - Ex. 94

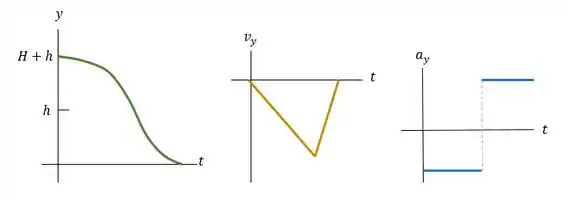
Aqueda da maçã de uma macieira pode ser considerada uma queda livre. A maçã está inicialmente a uma altura H acima do topo de um gramado espesso, o qual é constituído por camadas de grama de espessura h. Quando a maçã penetra na grama, ela diminui sua velocidade com uma taxa constante e atinge o solo com velocidade igual a zero. a) Ache a velocidade da maçã imediatamente antes de ela penetrar na grama. b) Ache a aceleração

da maçã enquanto ela penetra na grama. c) Faça gráficos y t , v y t e a y t para o movimento da maçã.

Passo 1

A maçã tem dois segmentos de movimento com aceleração constante. Para o movimento da árvore para o topo da grama a aceleração é g , para baixo e a maçã cai uma distância H - h .

Para o movimento de cima da grama para o chão a aceleração é para cima, desaceleranda a maçã, que viaja para baixo uma distância h, e o final a velocidade é zero.

Vamos tomar como + y para cima e seja y = 0 no chão.

A maçã é inicialmente uma altura H + h acima do solo.

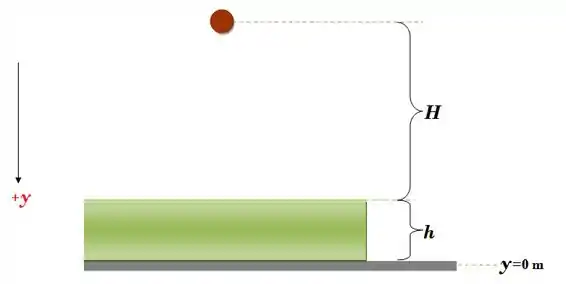
Passo 2

  1. Temos então, que o movimento:

    2. y 0 = H + h para y = H

    ⇒ y - y 0 = - H

    Temos que: v 0 y = 0 a y = - g

    E como não nos pede e não temos o tempo, t , podemos utilizar a equação de Torricelli para encontrar v y :

    v y 2 = v 0 y 2 + 2 a y ( y - y 0 )

    v y 2 velocidade final

    v 0 y velocidade inicial

    a y aceleração

    y posição final

    y 0 posição inicial

    v y 2 = 0 + 2 g ( H )

    ⇒ v y = 2 g H

    A velocidade da maçã é 2 g H quando penetra na grama.

    Passo 3

  2. Agora, temos que o movimento:

    3. y 0 = h para y = 0

    ⇒ y - y 0 = - h

    E agora temos que: v 0 y = 0 a y = - g v y = - 2 g H

    E utilizando, novamente a equação de Torricelli, encontraremos a aceleração da maçã:

    v y 2 = v 0 y 2 + 2 a y ( y - y 0 )

    v y velocidade final

    v 0 y velocidade inicial

    a y aceleração

    y altura final

    y 0 altura inicial

    Isso nos dá que:

    a y = v y 2 - v 0 y 2 2 ( y - y 0 ) = - 2 g H 2 ( - h ) = g H h

    A aceleração da maçã enquanto está na grama é g H / h , para cima.

    Passo 4

  3. A aceleração, a y , produzida pela grama aumenta quando H aumenta e diminui quando   h   aumenta.

Resposta

  1. A velocidade da maçã é 2 g H quando penetra na grama.
  2. A aceleração da maçã enquanto está na grama é g H / h , para cima.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A velocidade de um objeto é dada por v x t = α - β t 2 , onde α = 4,0m / s e β = 2,0m / s 3 . Para t = 0 , o objeto está em x = 0 . a) Calcule a posição e a aceleração do objeto em função do tempo. b)
2.10 Uma professora de física sai de sua casa e se dirige a pé para o campus. Depois de 5 min começa a chover e ela retorna para casa. Sua distância da casa em função do tempo é indicada pelo gráfico
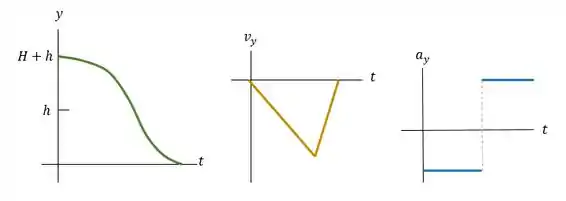
2.11 Uma bola se move em linha reta (eixo Ox). O gráfico na Figura 2.33 mostra a velocidade dessa bola em funç��o do tempo. a) Qual é a velocidade escalar média e a velocidade média nos primeiros 3,0
2.9 Um carro para em um semáforo. A seguir ele percorre um trecho retilíneo de modo que sua distância ao sinal é dada por x t = b t 2 - c t ³ ³, onde b=2,40m / s ² ² e c=0,120m / s ³ ³ . a) Calcule a
2.15 Uma tartaruga se arrasta em linha reta, à qual chamaremos de eixo O x com a direção positiva para a direita. A equação para a posição da tartaruga em função do tempo é x ( t )=50,0c m+( 2,0c m /