Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 7.Problemas Adicionais - Ex. 77
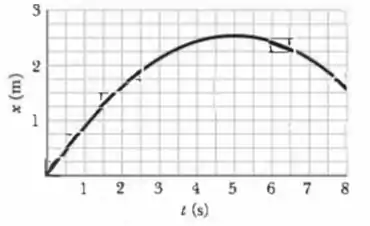
Uma merendeira de escorrega em uma superfície sem atrito no sentido positivo de um eixo . A partir do instante , um vento constante aplica uma força à merendeira no sentido negativo do eixo . A Fig. 7-49 mostra a posição da merendeira em função do tempo . A partir do gráfico, estime a energia cinética da merendeira (a) em e (b) em . (c) Qual é o trabalho realizado pelo vento sobre a merendeira entre e ?
Passo 1
O enunciado nos diz que a força que atua sobre a merendeira é constante, logo, já podemos afirmar que a aceleração da merendeira é constante, por isso, este é um MRUV. Lembrando que a função horária da posição é:
Passo 2
Agora, para determinar as variáveis e estruturar nossa expressão, vamos usar pontos do gráfico. De cara, podemos perceber que a função começa na origem, logo .
Usando o ponto :
E :
Isolando o na primeira expressão:
E substituindo na segunda expressão:
Isolando :
Passo 3
Com o valor da aceleração em mãos, podemos determinar o módulo da força resultante do vento através da segunda lei de Newton:
Passo 4
Como o enunciado pede a energia cinética em e vamos usar o teorema trabalho-energia cinética para determinar o valor da energia, então devemos primeiro determinar o trabalho da força do vento. Para tanto, devemos perceber que por ser uma força constante, podemos usar a seguinte relação para determinar o trabalho:
O deslocamento total no instante pode ser estimado pelo gráfico em . Sabendo também, como dito no enunciado, que a força age no sentindo contrário ao deslocamento e, portanto, , então:
Passo 5
Para usarmos o teorema trabalho-energia cinética, devemos perceber que ele não falou nada sobre a velocidade inicial da merendeira. Porém, para determinar a aceleração escrevemos a que é uma expressão que relaciona a velocidade inicial com a aceleração, como já calculamos a aceleração, então podemos determinar a velocidade inicial:
Passo 6
Por fim, usando o teorema trabalho-energia cinética:
Isolando :
Passo 7
Agora, vamos calcular o trabalho novamente, porém até o instante . Pelo gráfico podemos estimar que . Assim usando a expressão do trabalho já enunciado anteriormente:
Passo 8
Aplicando novamente o teorema trabalho-energia cinética:
Passo 9
Por fim, para determinar o trabalho da força do vento entre os instantes e , podemos aplicar novamente o teorema trabalho-energia cinética tendo em vista que já calculamos e . Então:
Resposta
- ;
- ;
- .