Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 11.Problemas - Ex. 70
Uma mesa uniforme de 90,0 N possui 3,6 m de comprimento, 1,0 m de altura e 1,2 m de largura. Um peso de 1500 N é colocado a 0,50 m de uma das extremidades da mesa, a uma distância de 0,60 m de cada uma das duas pernas nessa extremidade. Desenhe um diagrama do corpo livre para a mesa e ache a força que cada uma das quatro pernas exerce sobre o piso.
Passo 1
Fala aí, galerinha!
Nesse problema temos uma mesa uniforme de que possui de comprimento, de altura e de largura.
Um peso de é colocado a de uma das extremidades da mesa, a uma distância de de cada uma das duas pernas nessa extremidade.
A partir dessa situação temos que desenhar um diagrama do corpo livre para a mesa e achar a força que cada uma das quatro pernas exerce sobre o piso.
Tem ideia de como fazemos isso?
Nós vamos aplicar a primeira e segunda condição de equilíbrio para a mesa.
Ilustrando a mesa e os pontos, temos que:
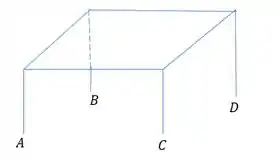
As pernas A e C estão separadas por . Deixe o peso ser colocado mais próximo
nas pernas C e D. Por simetria, e . Assim, temos que o diagrama de corpo livre é dado por:
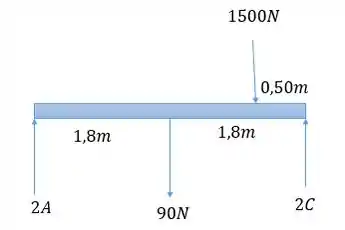
Veja só!
Passo 2
Aplicando sobre extremidade direita.
Isso nos dá que:
E então:
Tranquilo até aqui?
Passo 3
Agora vamos aplicar:
Isso nos dá que:
Show!
Passo 4
Usando:
E
Ficamos com:
Pela terceira lei do movimento de Newton, as forças A, B, C e D na mesa são da mesma magnitude que as forças que mesa exerce no chão.
E aí! o que achou? Responde Aí!
Resposta
e