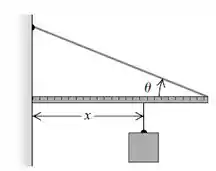
Uma extremidade de uma régua milimetrada é colocada contra uma parede vertical (Figura 11.50). A outra extremidade é mantida por uma corda de peso desprezível que faz um ângulo com a régua. O coeficiente de atrito estático entre a extremidade da régua e a parede é igual a . a) Qual é o valor do ângulo máximo para que a régua se mantenha em equilíbrio? b) Considere . Um bloco com a mesma massa da régua é suspenso da régua a uma distância da parede, conforme indicado. Qual deve ser o valor mínimo de para o qual a régua permaneça em equilíbrio? c) Quando , qual deve ser o coeficiente de atrito estático, de modo que o bloco possa ser amarrado a da parede sem que a régua escorregue?

a) Vamos aplicar a equação de equilíbrio dos torque, , para o bastão milimetrado (régua).

Nós sabemos que a parede exerce uma força estática de atrito estático positiva e uma força normal horizontal na régua. Então, nossa força de atrito será dada por:

Tomando torques na extremidade direita da régua, teremos:

Ou seja, a força de atrito é metade do peso do bastão.

Agora tomando os torques sobre o ponto em que o cabo está conectado à parede (a tensão no cabo e a força de atrito não exerce torque sobre esse ponto), e observando que o momento do braço da força normal é (onde é comprimento do cabo), temos:

Comparando isso com o nosso coeficiente de atrito entre a extremidade da régua e a parede, isso implica que:

Então, calculando o arco tangente para esse ângulo, temos:

b) Tomando os torques, como no item a) e considerando as forças e atuantes, temos:

E

Em termos do coeficiente de atrito , teremos então:

Resolvendo para , obtemos:

c) Na expressão acima, tomando e resolvendo para :

Valeu, galera! Até a próxima! 😉