Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 11.Problemas - Ex. 69

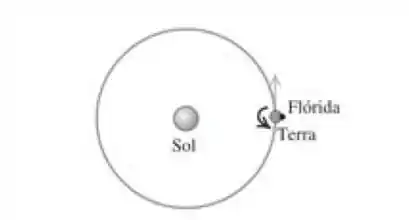
Desejamos lançar uma espaçonave da superfície da Terra de modo que ela também escape do sistema solar. a) Calcule a velocidade relativa ao centro com a qual ela deve ser lançada. Considere os efeitos gravitacionais do Sol e da Terra e inclua o efeito da velocidade orbital da Terra, mas despreze a resistência do ar. b) A rotação da Terra pode auxiliar a atingir esta velocidade de escape. Calcule a velocidade que a espaçonave deve possuir em relação à superfície da Terra se a espaçonave for lançada da Flórida no ponto indicado na Figura 12.37. A rotação da Terra em torno do seu eixo e seu movimento orbital em torno do Sol possuem o mesmo sentido de rotção. Em Cabo Canaveral um lançamento ocorre na latitude de 28,5 ° ao norte do equador. c) A European Space gency (ESA) utiliza uma plataforma de lançamento Guiana Francesa (imediatamente ao norte do Brasil). Situada a 5,15 ° ao norte do equador. Com que velocidade em relação à superfície da Terra deve uma espaçonave ser lançada da plataforma de lançamento na Guiana Francesa para que ela escape do sistema solar?

Passo 1

Opa, bora resolver esse problema! Nesse problema a gente vai lançar uma espaçonave da superfície da Terra de modo que ela também escape do sistema solar.

Temos que, na velocidade de fuga:

E = K + U = 0

Na superfície da Terra, o satélite está a uma distância: R T = 6,38 × 10 6   m do centro da Terra e a uma distância R T S = 1,50 × 10 11   m do Sol.

A velocidade orbital da Terra é 2 π R T S T , onde T = 3,156 × 10 7   s é o período orbital. A velocidade de um ponto na superfície da Terra em um ângulo φ do equador é:

v = 2 π R T cos ⁡ φ T ,

onde T = 86.400   s é o período de rotação da Terra.

Passo 2

  1. A velocidade de escape será:

    2. v = 2 G   m T R T + m s R T S = 4,35 × 10 4 m s .

    Assumindo que a direção do lançamento é a direção do movimento da Terra em sua órbita, a velocidade relativa ao centro da Terra é:

    v - 2 π R T S T = 4,35 × 10 4 m s - 2 π 1,50 × 10 11   m 3,156 × 10 7   s = 1,37 × 10 4   m / s .

    Passo 3

  2. A velocidade de rotação em Cabo Canaveral é

    3. 2 π 6,38 × 10 6   m cos ⁡ 28,5 ° 86,400   s = 4,09 × 10 2   m / s ,

    então a velocidade relativa à superfície da Terra é de 1,33 × 10 4   m / s .

    Passo 4

  3. Na Guiana Francesa, a velocidade de rotação é de 4,63 × 10 2   m / s ; portanto, a velocidade relativa à superfície da Terra é de 1,32 × 10 4   m / s .

A velocidade orbital da Terra é uma grande fração da velocidade de escape, mas a velocidade rotacional de um ponto na superfície da terra é muito menor.

Resposta

  1. 1,37 × 10 4   m / s
  2. 1,33 × 10 4   m / s
  3. 1,32 × 10 4   m / s
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Você abre um restaurante e deseja atrair clientes pendurando uma placa externa (Figura 11.37). A viga horizontal homogênea que sustenta a placa tem 1,50 m de comprimento, massa de 18,0 kg e está presa
Uma viga de massa M e comprimento L é horizontalmente sustentada nas suas extremidades por dois cabos que formam ângulos θ e ϕ com o teto horizontal (Figura 11.41). a) Mostre que,se a viga for homogên
Um caminhão picape possui uma base de roda ou distância entre os eixos igual a 3,0 m. Em geral, 10780 N se apóiam sobre as rodas dianteiras e 8820 N sobre as rodas traseiras quando ocaminhão está esta
A extremidade A da barra A B da Figura 11.39 repousa sobre uma superfície horizontal sem atrito, e a extremidade B está articulada. Uma força horizontal F → de módulo igual a 120N é aplicada à extremi
Uma placa retangular uniforme com largura d , altura h e peso p está suspensa com seus lados superior e inferior na horizontal (figura 11.48 ). No canto inferior esquerdo, há uma dobradiça, e no canto