Enunciado
Física - Moysés - Vol. 2 - Ed: 4º - Capítulo 9.Problemas - Ex. 6
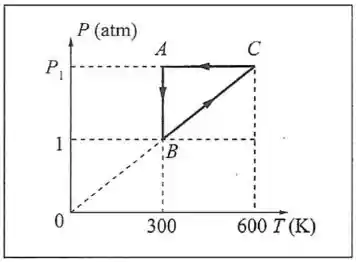
mol de um gás ideal, com , descreve o ciclo representado na figura no plano . (a) Represente o ciclo no plano , indicando (em atm) e (em ) associados aos pontos , e . (b) Calcule , e para os processos , , e o ciclo.
Passo 1
(a) O processo é isotérmico, e a pressão está caindo de um valor até . No plano isso terá a seguinte forma:
No processo a temperatura aumenta até ao longo de uma reta (isso indica um processo isovolumétrico), e a pressão volta ao valor .
E depois disso, para fechar o ciclo, podemos simplesmente voltar ao ponto , então:
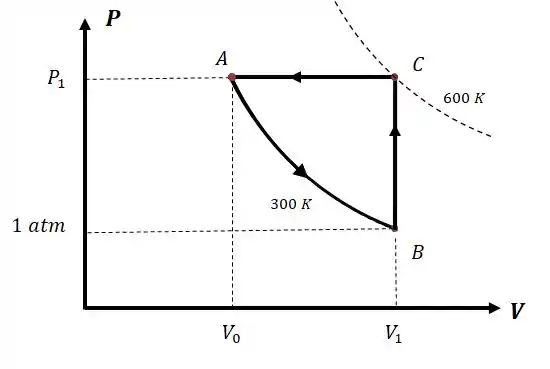
Agora falta completar o gráfico com os valores de , e .
Passo 2
Vamos começar olhando para o ponto para calcular :
Agora vamos comparar os pontos e para calcular :
E agora podemos olhar para o ponto para calcular :
Agora podemos colocar esses valores no gráfico:
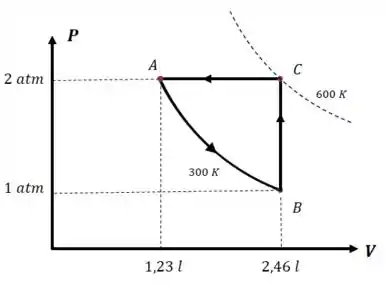
Passo 3
(b) Agora vamos calcular o trabalho , o calor e a variação de energia interna envolvidos em cada etapa.
Começando pelo trecho , que é um processo isotérmico.
E a fórmula para o trabalho realizado pelo gás em um processo isotérmico:
E então, pela primeira lei da termodinâmica:
Passo 4
Agora vamos considerar o trecho , que é um processo isovolumétrico:
E a fórmula para a variação de energia interna é:
Então, pela primeira lei da termodinâmica:
Passo 5
E por fim vamos considerar o trecho , que é um processo isobárico.
Podemos usar a mesma fórmula de antes para o cálculo da variação de energia interna:
E para calcular o trabalho (temos que usar a pressão em pascal e o volume em metros cúbicos):
Então, pela primeira lei da termodinâmica:
E para o ciclo completo, só precisamos somar todos os valores que calculamos:
Resposta
(a) Ver desenho.
(b) , e ; , e ; , e . Para o ciclo completo: , e .