Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 4.3 - Ex. 9
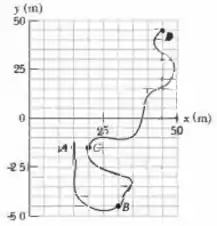
A mostra os movimentos de um esquilo em um terreno plano, do (no instante ) para os (em ), (em ) e, finalmente, (em ). Considere as velocidades médias do esquilo do ponto para cada um dos outros três pontos. Entre essas velocidades médias determine (a) o módulo e (b) o ângulo da que possui o menor módulo e (c) o módulo e (d) o ângulo da que possui o maior módulo.
Passo 1
Antes de se assustar com todas essas coordenadas vamos verificar o valor delas olhando para a figura. Assim, temos:
Todos esses pontos estão em metros, certo? Então vamos mudar esse tempo que está em minutos para segundos, pode ter certeza que vai facilitar sua vida daqui a pouco.
Passo 2
Agora que temos os valores necessários para nossos cálculos vamos para a resolução de (a). Essa alternativa pede qual velocidade média possui menor módulo (lembrando que todas velocidades são calculadas a partir de ). Apenas de olhar para a figura podemos ver que o ponto possui menor deslocamento em relação à . Calculando a velocidade média nesse ponto temos:
Como o resultado anula o componente em ,o módulo dessa velocidade é ela mesma.
Passo 3
Para (b) vamos usar a função inversa da... ACHOU ERRADO. Temos apenas a componente em meu jovem gafanhoto, o ângulo em relação a é igual a .
Passo 4
Olhando para a figura mais uma vez podemos responder (c). A maior velocidade média será no ponto , pois seu deslocamento é maior proporcionalmente que o ponto , assim seu módulo será:
Passo 5
Agora sim em (d) usaremos a função inversa da tangente para obtermos a resposta desejada.
***Nesse caso podemos usar os valores das componentes do deslocamento assim como a da velocidade, pois elas duas são divididas por um mesmo número para chegar na velocidade. Então proporcionalmente, no fim ficam “elas por elas”. Pode testar o resultado usando a velocidade média e o deslocamento, eles são iguais.
Resposta
- (b) (c) (d)