Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 3.1 - Ex. 25
Verdadeiro ou falso:
(a) Se a rapidez de um objeto é constante, então sua aceleração deve ser nula.
(b) Se a aceleração de um objeto é nula, então sua rapidez deve ser constante.
(c) Se a aceleração de um objeto é nula, então sua velocidade deve ser constante.
(d) Se a rapidez de um objeto é constante, então sua velocidade deve ser constante.
(e) Se a velocidade de um objeto é constante, então sua rapidez deve ser constante.
Passo 1
(a) A rapidez é o módulo da velocidade.
Sempre que houver alguma mudança na velocidade, seja em magnitude (rapidez), direção ou sentido, podemos ter certeza de que a aceleração não é nula.
O fato de que a rapidez é constante não garante que a aceleração é nula, pois a direção e/ou o sentido podem estar variando.
Um exemplo disso é uma partícula em trajetória circular mas que tem a rapidez constante de módulo :
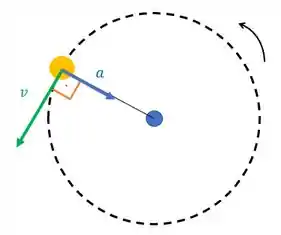
Há uma aceleração perpendicular a velocidade, que chamamos de centrípeta, para que essa partícula continue na trajetória circular. Ou seja, essa aceleração está mudando o sentido e a direção da velocidade de módulo .
Então a afirmação é falsa.
Passo 2
(b) Se a aceleração de um objeto é nula, isso quer dizer que tanto a direção, quanto a magnitude, quanto o sentido da velocidade se mantêm constantes, porque não há aceleração para modifica-los.
Sendo assim, a rapidez que é o módulo da velocidade vai ser, de fato, constante.
Então a afirmação é verdadeira.
Passo 3
(c) Aqui a gente pode usar o mesmo raciocínio da anterior. O papel da aceleração é mudar características da velocidade, sua magnitude, sentido ou direção.
Se não há aceleração, a velocidade permanece a mesma, ou seja, permance constante.
Uma outra forma de ver é olhando a definição de aceleração:
A aceleração é a derivada da velocidade. Ou seja, ela é a taxa de variação da velocidade. Se a velocidade muda de alguma forma, há uma variação, se há uma variação, a taxa de variação é não nula.
Assim, se a velocidade de um objeto não fosse constante, então por definição haveria alguma aceleração, porque haveria variação na velocidade.
E se não há variação na velocidade, a aceleração é nula.
Ou seja, a afirmativa é verdadeira.
Passo 4
(d) A velocidade é uma grandeza vetorial. Isso quer dizer que ela tem 3 características: módulo, direção e sentido.
Para ela ser constante, todas essas caraterísticas não podem mudar.
A rapidez é o módulo da velocidade. Ou seja, é só uma dessas características. Mesmo se ela for constante, a velocidade pode estar variando em direção e/ou sentido.
Assim, ter a rapidez constante não garante que o vetor velocidade seja constante.
A afirmação é falsa.
Passo 5
(e) Vimos no item anterior que para que uma velocidade (que é um vetor) seja considerada constante, ela precisa ter módulo, direção e sentido constantes. Se qualquer um desses fatores variar, já não podemos dizer que a velocidade é constante.
Como a rapidez é o módulo da velocidade, se a velocidade for constante, a gente pode ter certeza que a rapidez (o módulo da velocidade) também é.
Portanto, a afirmação é verdadeira.
Resposta
(a) Falso;
(b) Verdadeiro;
(c) Verdadeiro;
(d) Falso;
(e) Verdadeiro;