Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 3.1 - Ex. 13
Imagine jogar um dardo na vertical para cima, de forma que ele grude no teto. Depois de deixar a sua mão, ele reduz sua rapidez enquanto sobe até grudar. (a) Desenhe o vetor da velocidade do dardo nos tempos e , onde e ocorrem após ele deixar sua mão, mas antes de atingir o teto, e é um valor pequeno. A partir do seu desenho, encontre a direção da mudança na velocidade , e portanto a direção do vetor aceleração. (b) depois de ficar preso no teto por alguns segundos, o dardo cai em direção ao chão. Enquanto cai, a sua rapidez aumenta até atingir o chão. Repita a parte (a) para encontre a direção do seu vetor aceleração enquanto cai. (c) Agora imagine jogar o dardo horizontalmente. Qual é a direção do seu vetor aceleração após deixar a sua mão, mas antes de atingir o chão?
Passo 1
(a) Vamos desenhar as velocidades e , sabendo que as duas acontecem antes do dardo grudar no teto.
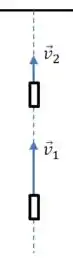
O mais importante nesse desenho é perceber que o vetor é menos comprido do que , o que representa a redução na rapidez do dardo pelo efeito de .
Para encontra só precisamos fazer a diferença dos dois vetores:
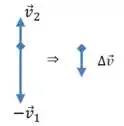
Passo 2
(b) Agora vamos fazer os mesmos dois desenhos, mas para a parte do movimento em que o dardo está caindo.
Começamos com os dois vetores e :
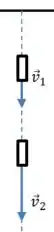
Dessa vez o vetor mais comprido está em um ponto mais baixo da trajetória. Agora vamos fazer a diferença dos dois vetores:
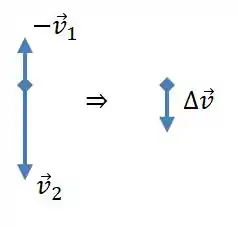
Perceba que o vetor aponta na mesma direção nos dois casos! Isso acontece porque a aceleração que age sobre o dardo é a mesma nos dois casos: a aceleração gravitacional, que sempre aponta na vertical para baixo.
Passo 3
(c) Jogando o dardo na horizontal, nada muda no vetor aceleração que age sobre ele durante o movimento: continua sendo vertical para baixo em todos os instantes desde que sai da sua mão até antes de tocar o chão.
Isso acontece porque a aceleração produzida pela gravidade é praticamente constante em qualquer lugar na superfície da Terra.
Resposta
(a) Desenho; (b) Desenho; (c) A aceleração continua sendo vertical para baixo, por ser exclusivamente gravitacional.