Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 11.Exercícios e Problemas - Ex. 67
67. O motor de um carro de fornece uma potência máxima de , porém dela é perdida antes de chegar ao eixo das rodas. O carro possui um perfil frontal com de largura e de altura. O coeficiente de atrito de rolamento é de . Qual é o valor da velocidade máxima do carro? Sua resposta é plausível?
Passo 1
Opa! Aqui vamos nós de novo!
Olha só! Nessa questão, assim como nas duas questões anteriores, o segredo é trabalhar com potência instantânea... Para fazer isso, basta multiplicar a força atuante pela velocidade .
Sendo assim, a nossa potência resultante vale...
Bom! Para se obter a força do carro, precisamos levar em consideração duas coisas...
A primeira é que temos o efeito do atrito de rolamento, cuja intensidade é dada por
A segunda é que podemos modelar o carro como um paralelepídepo, de modo que a força atuante sobre ele pode ser simplificada por...
Desse modo, a nossa força do carro vai ser dada pela soma dessas duas forças anteriores...
E a potência fica do seguinte jeito...
Substituindo os valores numéricos, chegamos até a seguinte equação... Lembrando que da potência do carro é perdida;
Passo 2
Essa é a equação que teremos de resolver...
Pra fazer isso, vamos usar um método iterativo chamado método da bissecção...
O método da bissecção é um método de busca de raízes que separa repetidamente um intervalo e então seleciona um subintervalo contendo a raiz para processamento adicional.
E o algoritmo da método da bissecção é o seguinte...
Pro nosso código não ficar tão extenso, vamos começar testando um intervalo. Sla! Que tal o intervalo entre e ...
Logo, há uma raiz nesse intervalo. Sabemos disso porque um valor deu positivo e o outro deu negativo! Bora pegar esse intervalo pra servir de referência
Sendo assim, o seguinte código abaixo foi confeccionado em , pegando um erro de parada de .
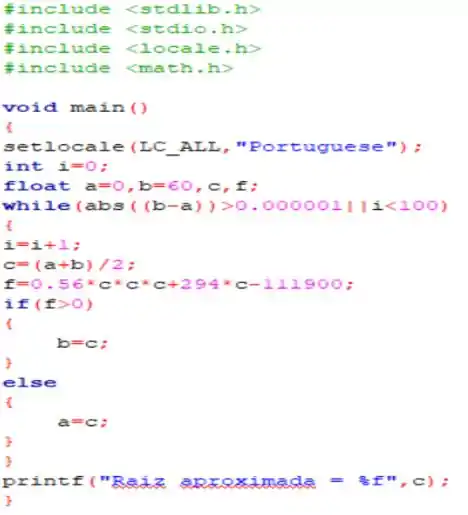
E o resultado da compilação foi...
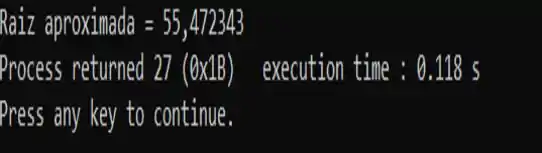
Ou seja, a nossa raiz é igual a aproximadamente .
E sim! A resposta é plausível! Um carro pode chegar a essa velocidade!