Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 18.Problemas Adicionais - Ex. 87
Um novato só pode entrar para o semi-secreto clube “””* da Estação Polar Amundsen-Scott, no Polo Sul, quando a temperatura do lado de fora está abaixo de . Em um dia como esse, o novato tem que fazer uma sauna e depois correr ao ar livre usando apenas sapatos. (Naturalmente, fazer isso é muito perigoso, mas o ritual é um protesto contra os riscos da exposição ao frio.) Suponha que, ao sair da sauna, a temperatura da pele do novato seja e que as paredes, teto e piso da base estejam a uma temperatura de . Estime a área da superfície do novato e suponha que a emissividade da pele é . (a) Qual é a taxa líquida, , com a qual o novato perde energia através da troca de radiação térmica com o aposento? Em seguida, suponha que, ao ar livre, metade da área de superfície do recruta troca energia térmica com o céu à temperatura de e que a outra metade troca radiação térmica com a neve e o solo à temperatura de . Qual é a taxa líquida com a qual o recruta perde energia através da troca de radiação térmica (b) com o céu e (c) com a neve e o solo?
* O nome se refere a uma diferença de entre a temperatura da sauna e a temperatura do lado de fora da base. (N. T.)
Passo 1
Ok, nossa primeira tarefa é estimar a área de superfície do novato. Não precisa ser muito exato, se estiver na mesma ordem de grandeza já é razoável. Uma forma interessante de modelar uma pessoa é fingir que ela é um cilindro com uma esfera em cima:
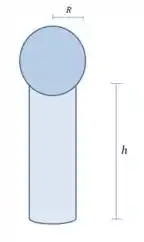
Como estamos falando de uma estação americana no Polo Sul, vamos fingir que o novato é um homem de (a média da altura nos EUA é , mas vamos arredondar pra cima).
Vamos dizer que o raio do cilindro é , e o da esfera que representa a cabeça é .
Então, a área da superfície (em metros cúbicos) é:
Passo 2
(a) Agora que fizemos a estimativa, o problema é o seguinte: qual é a taxa líquida com que a pessoa perde energia através de trocas de radiação térmica com o ambiente?
A dica está naquele termo: “líquida”, quer dizer que precisamos pensar em uma diferença! Nesse caso, a diferença entre a radiação absorvida e a emitida. Lembra das fórmulas?
E a diferença entre elas vai ser:
A emissividade foi dada na questão, e o é uma constante conhecida. Além disso, vamos usar a área que nós estimamos:
Falta converter as temperaturas para Kelvin! ( é a temperatura ambiente e é a temperatura do corpo)
Não se preocupe, ninguém faz essa segunda conversão de cabeça, em uma prova com certeza te dariam a fórmula. Voltando na equação:
Esse sinal negativo quer dizer que ele está emitindo mais do que absorve! Então a taxa com que o “novato” perde energia é:
Passo 3
(b) Agora nós vamos supor o seguinte: se metade do corpo troca energia com um ambiente de temperatura e a outra metade troca energia com um ambiente de temperatura .
Então basicamente é só fazer a mesma conta de antes duas vezes, só que usando a metade da área em cada uma, e trocando a temperatura.
A primeira metade vai ter essa taxa líquida aqui:
O sinal de menos indica perda de energia! Então a taxa com que o “novato” perde energia através da troca de radiação com o céu é:
Passo 4
(c) Agora é só seguir a mesma lógica:
A única coisa que muda é a temperatura ambiente, agora é
Então a taxa de perda de energia:
Resposta
(a)
(b)
(c)