Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 20.Problemas Adicionais - Ex. 56
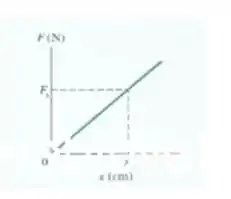
A figura abaixo mostra o módulo da força em função da distensão de um elástico com a escala do eixo definida por e a escala do eixo definida por . A temperatura é . Quando o elástico é distendido de , qual é a taxa de variação da entropia do elástico com a distensão para pequenas distensções?
Passo 1
Essa questão parece ser complicada, mas vou deixar ela mais fácil =D Vamos lá?
O problema pede a taxa ( leia-se razão) da variação de entropia (vai ser o numerador) com a distensão (denominador) para pequenas distensões. Bom, já deu pra sacar que estamos falando de mola, certo? Então a primeira coisa que vou fazer é determinar a constante da mola, pois sem ela não fazemos muita coisa, não é?
Pelo gráfico: a inclinação da reta vai dar a constante da mola, assim, usando os valores das escalas teremos:
Ok?
Passo 2
Agora vamos pensar na variação de entropia:
Então temos que ela vai ser o calor (ou a forma de energia que o sistema estiver sendo submetido) dividido pela temperatura (fornecida no enunciado).
Então o que precisamos determinar é essa forma de energia que vai ali no numerador, cert?
Como o elástico está submetido à pequenas distensões, sabemos a energia envolvida:
Passo 3
Vamos substituir isso na variação da entropia?
Pronto? Ainda não! Lembra do passo , onde falei quem vai estar no numerador e no denominador? Então, o que queremos é , então:
Agora sim! Basta substituir os valores!
Passo 4
Para uma distensão de temos: