Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 12.2 - Ex. 42

No Exemplo da figura, suponha que o coeficiente de atrito estático μ s entre a escada e o piso é 0,53 . A que distância (como porcentagem do comprimento total da escada) o bombeiro deve subir para que a escada esteja na iminência de escorregar?

Passo 1

Considere as forças atuantes sobre a escada e sobre o bombeiro representadas na figura abaixo.

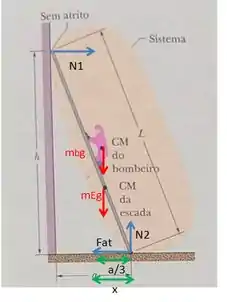
Primeiro, vamos nos lembrar que, na iminência de escorregar, a força de atrito atinge seu valor máximo, igual a F a t = μ × N . Aplicando o equilíbrio de forças na vertical e na horizontal, a gente tem as seguintes equações:

N 2 = m b g + m E g

N 1 = F a t = μ × N 2 = μ × g ( m b + m E )

Tal que m b e m E são as massas do bombeiro e da escada.

Passo 2

Do equilíbrio de torques com relação ao ponto de contato entre a escada e o piso, obtemos:

N 1 × h - m b g × ( x ) - m E g × a 3 = 0

Então, substituindo o valor de N 1 que encontramos no passo anterior, temos:

μ × g m b + m E × h - m b g × x - m E g × a 3 = 0

Passo 3

Agora, basta a gente isolar o valor de x acima e para encontrar o que a questão nos pede, basta dividi-lo por a .

x = μ × m b + m E × h - m E × a 3 m b

x a = μ × m b + m E × h - m E × a 3 m b × a

No exemplo dado no livro, a = 7,58   m , h = 9,3   m , m E = 45 k g   e m b = 72   k g . Então, temos que:

x a = 0,53 × 72 k g + 45   k g × 9,3   m - ( 45   k g ) × 7,58   m 3 m b × ( 7,58   m ) ≅ 0,848 = 84,8 %

Resposta

84,8 %

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma escada homogênea com 5,0m de comprimento e 400N de peso está apoiada em uma parede vertical sem atrito. O coeficiente de atrito estático entre o chão e o pé da escada é 0,46 . Qual é a maior distâ
Na Figura, o bloco A, com uma massa de 10k g , está em repouso, mas escorregaria se o bloco B , que tem uma massa de 5,0k g , fosse mais pesado. Se θ = 30 ° , qual é o coeficiente de atrito estático e
Um operário tenta levantar uma viga homogênea do chão até a posição vertical. A viga tem 2,50 m de comprimento e pesa 500 N. Em um certo instante, o operário mantém a viga momentaneamente em repouso c
Um cubo homogêneo de 8,0 cm de lado repousa em um piso horizontal. O coeficiente de atrito estático entre o cabo e o piso é μ . Uma força horizontal P → é aplicada perpendicularmente a uma das faces v
Uma escada homogênea tem 10 m de comprimento e pesa 200 N. Na Fig. 12-76, a escada está apoiada em uma parede vertical sem atrito a uma altura h=8,0 m acima do piso. Uma força horizontal F → é aplicad