Enunciado
Física - Young and Freedman - Vol 4- Ed: 12º - Capítulo 44.Exercícios - Ex. 26
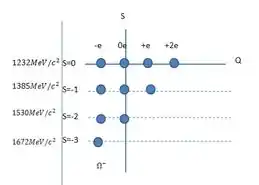
Nove bárions com spin são quatro partículas , cada uma delas com massa , estranheza e cargas , , e ; três partículas , cada uma delas com massa , estranheza e cargas e ; duas partículas , cada uma com massa , estranheza e cargas e .
- Coloque essas partículas em um gráfico de por . Deduza os valores de e de para o décimo bárion com spin /2, a partícula , e coloque-a em seu diagrama. Identifique as partículas com suas respectivas massas. A massa da partícula é ; esse valor está de acordo com seu diagrama?
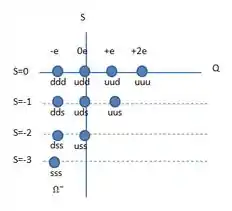
- Deduza as combinações de três quarks que compõem cada uma dessas dez partículas. Faça um novo desenho do gráfico de por do item (a) com cada partícula identificada com dísticos indicando seu respectivo teor de quark. Que regularidades você oberva?
Passo 1
Olá, tudo bem? Vamos resolver junto esse exercício? =D
Letra a)
O problema nos dá nove partículas, e são essas aqui:
- 4 partículas : .
- 3 partículas : .
- 2 partículas : .
Em um diagrama por , devemos alocar essas partículas por estranheza na vertical e cargas na horizontal, respeitando a ordem de colocação, saca só:
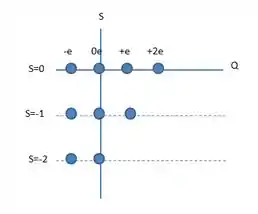
O décimo bárion terá e carga . Sabemos que sua massa é , o que está de acordo com o diagrama saca só:
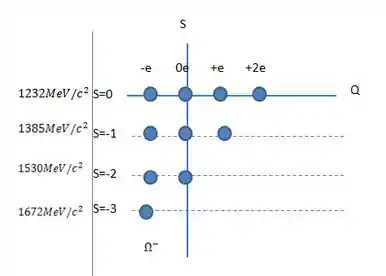
Coloquei nessa segunda figura as massas associadas a cada estranheza. Vemos que o valor de energia entre níveis é por volta de , então o valor do próximo nível de energia corrobora com isso =D
Passo 2
Letra b)
Agora vamos deduzir o teor de quark de cada uma dessas partículas. Devemos lembrar das cargas dos quarks e suas respectivas estranhezas:
Certo? Agora vamos organizar as partículas por partes, primeiro as partículas : temos , então vamos usar combinações de e apenas. Para obtermos cargas , combinando três quarks devemos ter o seguinte:
Agora para as partículas , lembrando que temos , logo devemos combinar também:
Agora para as partículas , que tem , então precisamos de dois , certo?
E para a décima partícula, temos apenas uma combinação possível, para o nível , que é , saca só:
E o diagrama da letra (a), mas agora com as combinações fica assim:
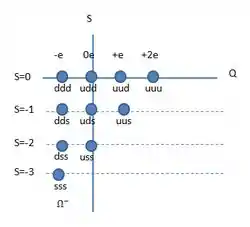
Beleza?
Espero ter ajudado!
Vamos pra próxima?
Resposta
