Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 9.Exercícios e Problemas - Ex. 56
O núcleo do isótopo do polônio (massa de 214 u) é radioativo e sofre decaimento emitindo uma partícula alfa (um núcleo de hélio com massa de 4 u). Através de experimentos de laboratório, mede-se a velocidade da partícula alfa como . Considerando que o núcleo de polônio esteja inicialmente em repouso, quanto vale a velocidade de recuo do núcleo remanescente após o decaimento?
Passo 1
Como o isótopo de Polônio emite a partícula alfa então temos um caso de separação de corpos o que é diferente de colisão de corpos. O que nos dá o diagrama abaixo.
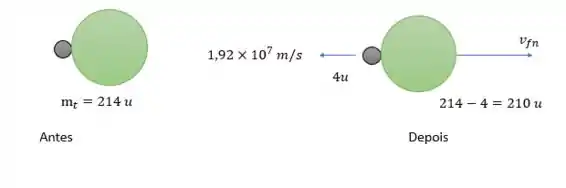
Onde devemos ver que a massa do núcleo remanescente será a massa do isótopo do polônio menos a massa da partícula alfa. Então essa massa será de
Passo 2
Agora não é por que houve essa separação que a conservação do momento linear falha. Nós teremos ainda que:
Ou seja:
Onde é a massa da partícula alfa, assim como é a velocidade inicial da partícula alfa, que nesse caso é nula e é a velocidade final do núcleo. Então:
Então a velocidade final do núcleo será igual a: