Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 9.Exercícios e Problemas - Ex. 53
Uma bomba de é arremessada a segundo um ângulo de acima da horizontal. A resistência do ar é desprezível. No ponto mais alto da trajetória, a bomba explode e se divide em dois fragmentos, um dos quais de massa quatro vezes maior que a do outro. O fragmento mais pesado aterrissa diretamente abaixo do ponto da explosão. Se a explosão exerce força apenas na direção horizontal, a que distância do ponto de lançamento aterrissa o fragmento mais leve?
Passo 1
Esse também é daqueles problemas divertidos e que você pode dividir em sistemas diferentes. O primeiro sistema é olhando somente para o lançamento oblíquo da bomba até o ponto mais alto da trajetória.
Nossa intenção aqui é descobrir a distância horizontal percorrida nesse lançamento e para isso precisamos da velocidade inicial vertical da bomba e que será de:
Enquanto a velocidade inicial horizontal é de:
E essa velocidade horizontal se manterá constante durante toda a trajetória.
Então precisaremos do tempo que a bomba percorre essa trajetória e pra isso precisamos de
A distância percorrida pela bomba é encontrada pela equação de Torricelli na sua altura máxima (onde a velocidade vertical é zero) e que será de:
Pois a aceleração da bomba será igual a gravidade que faz com que a velocidade vertical caia.
Então o tempo percorrido será achado por:
Então teremos a equação do segundo grau:
O que nos dá , outra forma de se calcular seria por .
Portanto a distância horizontal percorrida pela bomba nesse lançamento será de:
Passo 2
Aí a bomba explode
Deixando o sistema depois da explosão da seguinte forma:
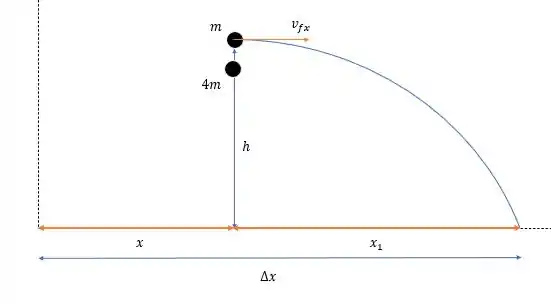
Onde a massa total da bomba é de e a velocidade inicial da bomba mais pesada é nula, uma vez que não há momento linear no eixo vertical no instante em que a bomba explode (já que a velocidade vertical no ponto mais alto da trajetória é nulo).
Então a velocidade horizontal da massa menor será de:
Dessa forma o tempo de queda da massa continua sendo de (uma vez que a distância não se altera e a velocidade vertical ainda continua sendo nula). Logo a distância horizontal percorrida pelo fragmento será de:
Então a distância horizontal total será de: