Um objeto curto e retilíneo, de comprimento , está no eixo central de um espelho esférico, a uma distância do espelho. (a) Mostre que a imagem do objeto no espelho tem um comprimento dado por

(b) Mostre que a ampliação longitudinal é igual a , em que é a ampliação lateral.

Fala galerinha, beleza?

Para começar essa questão, vamos fazer primeiro um desenho da situação:

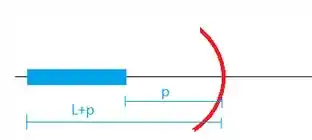
Vamos achar as posições das imagens correspondentes aos extremos da barra. Para a extremidade mais próxima do espelho, usamos

Assim,

Portanto,

Já para a extremidade mais afastada:

Assim,

O comprimento da imagem da barra é

Usei o módulo pois não sei quem é maior que quem entre e . Substituindo as expressões:

Assim,

Fazendo as distributivas:

Ou ainda,

Essa expressão é quase igual a mostrada no enunciado, com uma pequena mudança no denominador. Se considerarmos um limite em que , isto é, uma situação em que o comprimento da barra é muito menor que a distância da barra ao espelho, nós obtemos exatamente o resultado pedido pelo enunciado!