Enunciado
Física - Moysés - Vol. 4 - Ed: 1º - Capítulo 2.Problemas - Ex. 18
Um espelho esférico tem distância focal . Ache duas posições de um objeto para as quais o tamanho da imagem é vezes maior que o tamanho do objeto. Discuta todos os casos possíveis, conforme o espelho seja côncavo ou convexo e a imagem seja real ou virtual; em cada caso, desenhe o traçado de raios mostrando as posições de objetos e imagem em relação ao vértice e ao foco do espelho.
Passo 1
Bom, sabemos que para um espelho esférico, valem as relações para o aumento lateral:
No enunciado, foi dito que o tamanho da imagem deve ser vezes maior que o tamanho do objeto. Com isso, devemos ter .
Se , temos que (imagem virtual). Por outro lado, se , temos que e a imagem é real. Vamos tratar os dois casos.
Passo 2
Primeiro com :
Logo,
Por fim
Como (o enunciado disse claramente que a imagem é maior que o objeto), temos que
Com isso, vemos que o sinal de é o mesmo sinal de ! Como para objetos reais, devemos ter . Portanto, o espelho deve ser côncavo!
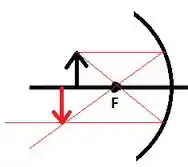
Vamos analisar com bastante calma essa situação. Primeiro, como , a imagem é direita. Com isso, nessa situação, a imagem formada pelo espelho concavo é direita, maior que o objeto e será virtual (pois ).
Note também que
pois . Assim, para que isso ocorra num espelho côncavo, o objeto deve estar entre o foco e o vértice do espelho, como mostrado na figura:
Passo 3
Agora vamos para o caso em que :
Portanto,
Logo,
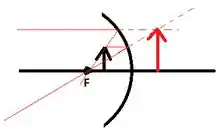
Novamente, como , devemos ter . Assim, essa situação também contempla espelhos côncavos! Basta lembrar que para espelhos convexos, objetos reais só produzem imagens menores, por isso eles não aparecem nesse problema...
Nesse caso, vamos ter (objeto antes do foco) e (imagem real):
