Enunciado
Física - Halliday - Vol 4- Ed: 10º - Capítulo 34.Problemas Adicionais - Ex. 115
Um objeto pontual está a de distância de um espelho plano, e o olho de um observador (cuja pupila tem de diâmetro) está a de distância. Supondo que o olho e o objeto estão na mesma reta perpendicular à superfície do espelho, determine a área do espelho envolvida na observação do reflexo do ponto. (Sugestão: Veja a Fig. 34-4.)
Passo 1
E aí meus caros(as)! A nossa missão agora é solucionar a questão 115!
Bem! E o que a gente tem aqui é mais uma exerciciozinho sobre formação de imagens em espelhos planos!
Para entender o que está acontecendo vamos dar uma olhada na figura abaixo...
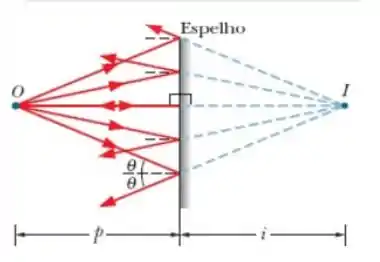
onsidere dois raios de luz, r e r, que estão acima e abaixo do raio normal (o raio que refaz o
Agora imagina que a gente tem dois raios de luz, e , que estão acima e abaixo do raio normal (o raio que refaz o percurso ao ser refletido). Os dois raios tem um ângulo de incidência igual a .
Suponha que os dois raios atingem a extremidade superior e a extremidade inferior da pupila depois de serem refletidos. Se o raio atinge o espelho no ponto A e o raio atinge o
espelho no ponto B, a distância entre A e B é dada por:
Onde é a distância do espelho ao objeto!
onsidere dois raios de luz, r e r, que estão acima e abaixo do raio normal (o raio que refaz
Passo 2
Podemos construir um triângulo retângulo tomando como um dos vértices a imagem do objeto (o ponto da imagem do ), situado a uma distância atrás do espelho
Um cateto do triângulo coincide com o raio normal (que liga o ponto ao centro da pupila), e a hipotenusa coincide com o raio (depois de refletido). E a distância entre a pupila e o olho é dada por , onde o menor ângulo do triângulo é ! Assim...
E é o raio da pupila, de . Sendo assim, combinando a fórmula anterior com a do :
Onde substituindo os valores numéricos;
Só que esse aí na real é o diâmetro de uma área circular do espelho tal que todos os raios refletidos em pontos dessa área chegam ao olho. Assim, a área abrangida será de...
Pronto! Ta aí a nossa resposta!