Enunciado
Física - Tipler - Vol 2- Ed: 6º - Capítulo 32.1 - Ex. 6
Os espelhos convexos são frequentemente usados para espelhos retrovisores em carros e caminhões para dar uma visão grande angular. ″ Aviso, os objetos estão mais próximos do que parecem. ″ Está escrito abaixo dos espelhos. No entanto, de acordo com um diagrama de raios, a distância da imagem para objetos distantes é muito menor do que a distância do objeto. Por que então eles parecem mais distantes?
Passo 1
Salve rapeize, como vocês estão? Vamo começar com uma visão geral do negócio, ok? Eles parecem mais distantes porque em um espelho convexo os tamanhos angulares das imagens são menores do que seriam em um espelho plano. O tamanho angular da imagem é dado por:
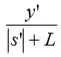
Passo 2
Usando essa equação e adaptando para Gauss, temos:
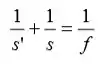
Isolando , temos:
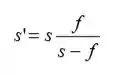
Como é negativo e é positivo (regra para espelho convexo), temos:
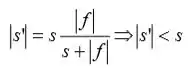
Provamos então que eles parecem mais distantes por causa da diferença de tamanho dos objetos.
Resposta
Provamos então que eles parecem mais distantes por causa da diferença de tamanho dos objetos.