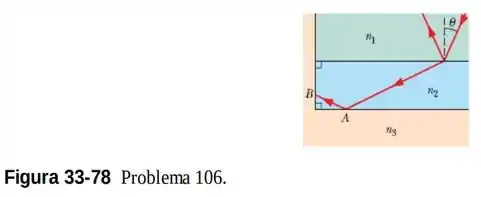
Na Fig. 33-78, em que e , a luzé refratada do material 1 para o material 2. Se a luz incide no ponto A com o ângulo crítico da interface dos materiais 2 e 3, determine (a) o ângulo de refração no ponto B e (b) o ângulo inicial . Se, em vez disso, a luz incide no ponto B com o ângulo crítico da interface dos materiais 2 e 3, determine (c) o ângulo de refração no ponto A e (d) o ângulo inicial . Se, em vez disso, a luz incide no ponto A com o ângulo de Brewster para a interface entre os materiais e , determine (e) o ângulo de refração no ponto B e (f) o ângulo inicial .
Passo 1
E aí meus caros(as)! Bora agora pra questão 106!
No primeiro item, a gente tem que descobrir o ângulo de refração no ponto !
a) Pois muito bem! Se liga! A gente tem que o ângulo de incidência no ponto B é o complemento do ângulo de incidência no ponto A, que por sua vez é o ângulo crítico...
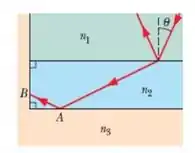
Logo, com base na figura acimo, temos que...
E assim, o ângulo de refração no ponto será dado pela expressão abaixo...
Onde substituindo os valores numéricos...
Obtemos o ângulo de refração em !
Passo 2
b) Em seguida, vamos tratar de obter o ângulo de incidência !
A gente consegue tirar a seguinte relação entre o ângulo de incidência e o ângulo crítico :
Só que pode ser escrito como:
Logo, ficamos com:
Substituindo os valores numéricos:
Conseguimos alcançar o nosso ângulo de incidência!
Passo 3
c) Seguindo em frente, vamos obter o ângulo de refração no ponto , considerando que a luz incide no ponto B com o ângulo crítico da interface dos materiais 2 e 3!
O ângulo de incidência no ponto A é o complemento do ângulo de incidência no ponto B, que, por sua vez, é o ângulo crítico... Ou seja:
E portanto, o ângulo de refração, , no ponto será de:
Sendo assim...
Passo 4
d) Quanto ao ângulo inicial de incidência ... Considerando a nova condição, temos que:
Só que do item anterior, sabemos que...
Logo;
E então, substituindo os valores numéricos:
Obtemos o ângulo de incidência pra esse caso!
Passo 5
e) A partir desse quinto item, a situação agora é um pouco diferente. Temos que considerar que a luz incide no ponto A com o ângulo de Brewster para a interface entre os materiais e .
Bom! O ângulo de incidência no ponto B é o complemento do ângulo de incidência no ponto A, que, por sua vez, é o ângulo de Brewster. Sendo assim, temos que:
E portanto, o ângulo de refração no ponto é:
Sendo assim:
Passo 6
f) Pra finalizar, falta obter o ângulo inicial !
Para fazer isso, bora usar a relação abaixo...
Onde...
Desse modo, temos que...
Resposta
a)
b)
c)
d)
e)
f)
da relação entre