Quando um objeto rola sem deslizar, a força de atrito de rolamento é muito menor que a força de atrito quando o objeto desliza sem rolar; uma moeda de um real rola sobre sua periferia mais rapidamente do que quando ela desliza com sua face voltada para baixo (veja a Seção 5.3). Quando um objeto rola sem deslizar ao longo de uma superfície horizontal, podemos desprezar a força de atrito, de modo que ax e az são nulos e vx e vz são aproximadamente constantes. Rolar sem deslizar implica vx rvz e ax raz. Quando um objeto se desloca sobre uma superfície sem obedecer a essas igualdades, o atrito (cinético) de deslizamento está atuando sobre o objeto à medida que ele desliza, até que o rolamento sem deslizamento comece a ocorrer. Um cilindro homogêneo de massa M e raio R girando com velocidade angular v0 em torno de um eixo passando em seu centro é lançado sobre uma superfície horizontal sobre a qual o coeficiente de atrito cinético é mc. (a) Faça um diagrama do corpo livre para o cilindro sobre a superfície. Pense com atenção no sentido da força de atrito sobre o cilindro. Calcule as acelerações ax do centro de massa do cilindro e a aceleração angular az em torno do centro de massa do cilindro. (b) No início o cilindro desliza sem rolar, então vz v0, mas vx 0. O rolamento sem deslizamento começa quando vx R vz. Calcule a distância que o cilindro percorre no momento em que o deslizamento termina. (c) Calcule o trabalho realizado pela força de atrito sobre o cilindro desde o momento em que ele toca a superfície até o momento em que começa o rolamento sem deslizamento
Passo 1
Vamos fazer mais uma questão!!
E aiii galera,
Letra a:
O diagrama de corpo livre está desenhado abaixo:
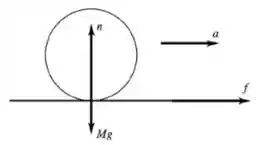
A força de atrito é
A magnitude da aceleração angular é:
Passo 2
Letra b:
Sendo
Temos,
Passo 3
Letra c:
A energia cinética final é:
Então, a variação de energia cinética é:
Resposta
- Ver resolução
- e