Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Young and Freedman - Vol 1- Ed: 14º - Capítulo 11.Problemas - Ex. 53

Em uma versão simplificada da ação da musculatura nos exercícios de levantamento de perna, os músculos abdominais puxam o fêmur (osso da coxa) para elevar a perna girando-a em torno de uma extremidade (Figura P11.53). Quando você está deitado horizontalmente, esses músculos formam um ângulo de aproximadamente 5° com o fêmur e, se você levantar suas pernas, os músculos permanecem aproximadamente horizontais, de modo que o ângulo u aumenta. Suponha, para simplificar, que esses músculos se conectem ao seu fêmur em apenas um ponto, a 10 cm da articulação do quadril (embora, na realidade, a situação seja mais complicada). Para uma pessoa de 80 kg com uma perna de 90 cm de comprimento, a massa da perna é de 15 kg e seu centro de massa está a 44 cm de seu quadril, conforme medido ao longo da perna. Se a pessoa levantasse sua perna a 60° acima da horizontal, o ângulo entre os músculos abdominais e seu fêmur também estaria em torno de 60°. (a) Com sua perna levantada a 60°, ache a tensão no músculo abdominal em cada perna. Desenhe um diagrama do corpo livre. (b) Quando a tensão nesse músculo é maior: quando a perna está levantada a 60° ou quando a pessoa começa a levantá- -la do solo? Por quê? (Experimente por si só.) (c) Se os músculos abdominais conectados ao fêmur fossem perfeitamente horizontais quando uma pessoa estivesse deitada, ela poderia levantar sua perna? Por quê?

Passo 1

E aii galera, vamos fazer mais uma questão?

Letra a:

A perna está em uma posição de equilíbrio, então a soma do torque é zero ∑ τ = 0 . O torque é aplicado devido à força de tensão T e o peso da perna W. A tensão é aplicada com um ângulo θ na distância 10 cm, enquanto o peso está a uma distância de 44 cm, conforme mostrado no diagrama de corpo livre abaixo. Assim, podemos obter a tensão:

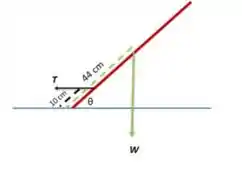
∑ τ = 0 0.10 m T sin ⁡ θ - 0.44 m W cos ⁡ θ = 0 T = 4.4 m g cos ⁡ θ sin ⁡ θ T = 4.4 m g tan ⁡ θ

Passo 2

Substituindo valores, temos:

T = 4.4 m g tan ⁡ θ = 4.4 15 k g 9.8 m s 2 tan ⁡ 60 ∘ = 373 N

Passo 3

Letra b:

Conforme mostrado pela primeira equação, a tensão é inversamente proporcional ao ângulo θ . Portanto, à medida que o ângulo diminui, a tensão aumenta. Então, a resposta é que a tensão é maior quando a pessoa começa a levantá-la do chão.

Passo 4

Letra c:

Quando os músculos abdominais estão horizontais ao fémur, o ângulo será 0. Então, a tensão na equação será:

T = 4.4 m g tan ⁡ 0 = 4.4 m g 0 = ∞

Portanto, a resposta é que a pessoa não conseguia levantar a perna quando os músculos abdominais são horizontais ao fêmur.

Resposta

  1. T = 373 N
  2. Quando a pessoa começa a levantá-lo do chão.
  3. A pessoa não conseguia levantar a perna
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A armação quadrada da Fig. 12-77 é formada por quatro barras laterais: AB, BC, CD e DA, e duas barras diagonais, AC e BD, que passam livremente uma pela outra no ponto E. Através do esticador G, a bar
Considere uma viga rígida de 2,5 m de comprimento (Figura 12-51), suportada em seu centro no topo de um poste fixo de 1,25 m de altura, podendo pivotar sobre um mancal sem atrito. Uma extremidade da v
A Figura 12-56 mostra uma barra de 5,00 kg, com 1,00 m de comprimento, articulada em uma parede vertical e suportada por um arame fino. O arame e a barra forma um ângulo de 45° com a vertical. Quando
Uma prancha de 3,0m , com 5,0k g de massa, é articulada em uma de suas extremidades. Uma força F → é aplicada verticalmente sobre a outra extremidade, e a prancha forma um ângulo de 30 ° com a horizon
Um cilindro de massa M está apoiado sobre uma calha sem atrito, formada por um plano inclinado de 30 ° com a horizontal, à esquerda, e outro plano inclinado de 60 ° , à direita, como mostrado na Figur