Enunciado
Física - Halliday - Vol 4- Ed: 10º - Capítulo 34.4 - Ex. 74
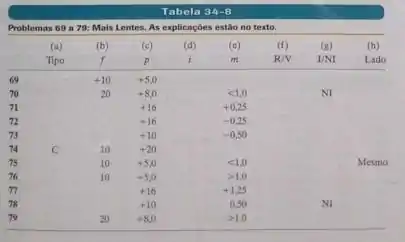
Um objeto está sobre o eixo central de uma lente delgada simétrica. Para cada problema, a Tabela 34-8 mostra o tipo de lente, convergente ou divergente , a distancia focal , a distancia do objeto , a distancia da imagem e a ampliação lateral . (todas as distâncias estão em centímetros.) A tabela também mostra se a imagem é real ou virtual , se é invertida ou não invertida e se está do mesmo lado da lente que o objeto ou está do lado oposto . Determine os dados que faltam, incluindo o valor de nos casos em que apenas uma desigualdade é fornecida. Nos casos em que está faltando apenas um sinal, determine o sinal.
Passo 1
Bom, as letras (a) e (c) já foram respondidas pela tabela, vamos para a (b) e depois para a (d). Como a lente é convergente, o sinal da distância focal é positivo.
Passo 2
(d) Usando a equação de lentes delgadas:
Podemos calcular , já que temos os valores de e :
Passo 3
(e) usando a equação de ampliação, a gente calcula usando o do passo anterior:
Passo 4
(f) Como , a imagem é real
Passo 5
(g) E já que , a imagem é invertida .
Passo 6
(h) A imagem sendo real, se forma do lado oposto da lente .