Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Tipler - Vol 2- Ed: 6º - Capítulo 32.1 - Ex. 56

Em uma forma conveniente da equação das lentes delgadas usada por Newton, as distâncias objeto e imagem x e x ' são medias a partir dos pontos focais F e F ' , e não a partir do centro da lente. (a) Indique x e x ' em um esboço de uma lente e mostre que se x = s - f e x ' = s ' - f , a equação das lentes delgadas (Equação 32-12) pode ser reescrita como x x ' = f 2 . (b) Mostre que a ampliação lateral é dada por m =   - x ' f =   - f x ·.

Passo 1

OPA, fala aí, tudo beleza? Espero que sim, vamos para mais uma questão! Podemos começar substituindo x = s - f e x ' =   s ' - f na equação das lentes delgadas e na equação para ampliação lateral de uma imagem para obter a equação de Newton, então, se liga na cara das equações que utilizaremos:

1 s + 1 s ' = 1 f (1)

m = - s ' s (2)

Agora iremos para o problema!

Passo 2

As variáveis x , f , s , e s ' são mostradas no rascunho abaixo:

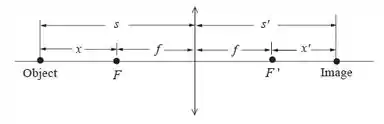
Expressando a equação (1) e substituindo s e s ' , temos:

1 s + 1 s ' = 1 f

1 x + f + 1 x ' + f = 1 f

Expandindo a expressão, obtemos:

f x ' + x + 2 f = x + f ( x ' + f )

f x ' + f x + 2 f 2 = x x ' + x f + x ' f + f 2

- x x ' = x f + x ' f + f 2 - f x ' - f x - 2 f 2

- x x ' = - f 2

x x ' = f 2 (3)

Dessa forma, resolvemos a parte (a)! Agora, vamos para parte (b), apertem os cintos!

Passo 3

Para a resolução da parte (b), começaremos expressando a equação (2) e substituindo s e s ' :

m =   - s ' s

m =   - x ' + f x + f

Resolvendo a equação (3) para x , temos:

x x ' = f 2

x = f 2 x '

Substituindo x na expressão de m , temos:

m =   - x ' + f f 2 x ' + f

m =   - x ' + f f f + x ' x '

m =   - x ' f

A ampliação lateral também pode ser dada, com x ' = f 2 x ·, logo:

m =   - f 2 x + f x + f

m =   - f f x + 1 x 1 + f x

m =   - f x

Com isso, chegamos à conclusão que m =   - x ' f =   - f x

PRONTINHO, Detonamos mais uma (toca aqui!), até a próxima, fica bem, beijosss!

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Obtenha a equação das lentes delgadas para uma lente de índice de refração n 2 situada entre dois meios de índices n 1 e n 3 . Verifique que o resultado se reduz ao que foi obtido, quando n 1 = n 3 .
Demonstre que a distância focal de uma lente delgada biconvexa pode ser expressa em função do diâmetro D da lente, de sua espessura t e do seu índice de refração n 12 relativo ao meio.
Se dermos um pequeno deslocamento Δ p à posição de um objeto, ao longo do eixo de uma lente delgada, a imagem desse objeto se desloca de Δ q . A razão Δ q / Δ p chama-se aumento longitudinal. Demonstr
Chama-se potência P de uma lente, o inverso de sua distância focal f (se f for medida em m , P se mede em d i o p t r i a s ). Considere duas lentes delgadas de potências P 1 e P 2 em contato uma com
Uma lente delgada biconvexa tem distância focal f .a) Demonstre que a distância mínima entre um objeto e sua imagem real é igual a 4 f . Para que distância p do objeto à lente esse mínimo é atingido?