Enunciado
Física - Moysés - Vol. 4 - Ed: 1º - Capítulo 2.Problemas - Ex. 23
Obtenha a equação das lentes delgadas para uma lente de índice de refração situada entre dois meios de índices e . Verifique que o resultado se reduz ao que foi obtido, quando .
Passo 1
Vamos usar a mesma ideia que usamos no problema 16 deste mesmo capítulo, considerando a expressão de uma superfície refratora esférica:
Primeiro consideramos a refração pela primeira superfície esférica:
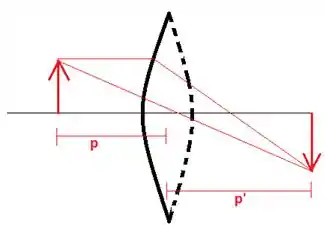
Usando a equação, e considerando que a imagem é formada “dentro” da esfera onde o índice é :
Assim,
Guarde essa equação!
Passo 2
Agora vamos olhar para a segunda refração, que acontece na outra superfície esférica:
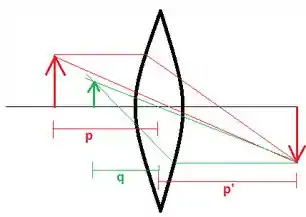
Agora, a imagem da primeira refração é o objeto virtual da segunda:
É importante ressaltar que o desenho é meramente ilustrativo e não condiz com a disposição real dos raios de luz e das posições das imagens formadas. Tivemos que usar o sinal negativo no pois trata-se de um objeto virtual e agora passamos do meio com índice para um meio com índice (mesmo que o desenho não represente isso).
Com isso, temos que
Passo 3
Igualando a equação do passo 1 com a equação do passo 2:
Daí,