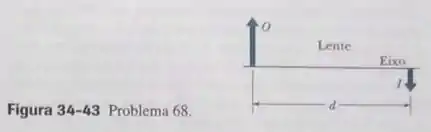
Na Fig. 34-43, uma imagem real invertida de um objeto é formada por uma lente (que não aparece na figura); a distância entre o objeto e a imagem, medida ao longo do eixo central da lente, é . A imagem tem metade do tamanho do objeto. Que tipo de lente é capaz de produzir a imagem? A que distância do objeto deve ser colocada a lente? Qual deve ser a distância focal da lente?

(b) Bom, a imagem tem metade do tamanho do objeto, então a ampliação é:

Além disso, o enunciado deu pra gente a distância entre o objeto e a imagem, como é a distância entre o objeto e a lente e é a distância entre a imagem e a lente, pode ser escrito assim:

Como queremos a distância do objeto, vamos isolar :

E substituir na equação de ampliação:

Isolando :

(c) Para acharmos a distância focal, vamos suar a equação de lentes delgadas:

Substituir como fizemos no passo 2:

Inverter os dois lados:

E usar o valor dado de e o que calculamos de :

vai ser: