Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 17.Problemas Adicionais - Ex. 109
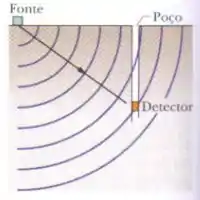
Os paleontólogos podem usar ondas sonoras para produzir uma imagem computadorizada do fóssil de um dinossauro incrustado na rocha. A imagem serve para guiar os paleontólogos durante a remoção do fóssil. (A técanica é mostrada nas cenas de abertura do filme Jurassic Park.) Para isso, um pulso sonoro de alta intensidade é emitido por uma fonte especial (um canhão sísmico) no nível do solo e detectado por hidrofones instalados em um poço a intervalos regulares. A fonte e um hidrofone são mostrados na figura. Se a onda sonora se propaga da fonte para o hidrofone apenas através da rocha, como na figura, ela viaja com uma velocidade e leva um certo tempo . Se, em vez disso, ela atravessa um osso fossilizado no caminho, leva um tempo ligeiramente maior, já que a velocidade de propagação no osso é menor do que na rocha. Medindo a diferença entre os tempos de percursos esperado e observado, a distância percorrida no osso pode ser calculada. Depois que esse procedimento é repetido para muitas localizações da fonte e dos hidrofones, um computador pode transofmar as várias distâncias calculadas em uma imagem do fóssi.
(a) Seja a velocidade do som no osso fossilizado, onde é muito menor que . Mostre que a distância é dada por:
(b) Para e , que valor típico de pode ser esperado se o som passar pelo diâmetro de um osso da perna de um T.rex adulto? (Estime o diâmetro do osso.)
Passo 1
Em um trecho em que a velocidade de uma onda é constante, podemos escrever o seguinte:
No caso em que não aparece nenhum osso no meio do caminho, e a onda percorre o caminho inteiro só com a mesma velocicdade , o tempo de percurso é:
No caso em que a onda percorre uma distância ao longo do osso com velocidade , o tempo de percurso total é:
Passo 2
(a) Então a diferença de tempo entre os dois caminhos é:
Agora vamos tentar isolar nessa equação:
Como é muito menor do que , podemos ter certeza de que o primeiro termo dentro do parênteses será muito maior do que o segundo, então podemos aproximar:
Passo 3
(b) Vamos supôr que o osso tenha um diâmetro , então teríamos:
Resposta
(a) Demonstração.
(b) O valor esperado para é de aproximadamente .