Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 13.Problemas Adicionais - Ex. 100
Quatro partículas iguais de são colocadas nos vértices de um quadrado com de lado. Qual é o módulo da força gravitacional que três dessas partículas exercem sobre a quarta partícula?
Passo 1
Vamos começar com um desenho da situação:
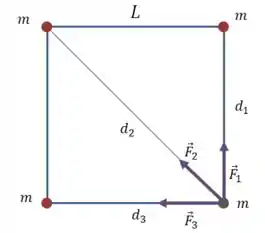
E vamos calcular a força que as três partículas vermelhas exercem sobre a verde (a escolha da partícula verde não muda o resultado final, já que o quadrado é simétrico).
Para cada par de partículas, o módulo da força segue a seguinte equação:
Passo 2
Pelo desenho, podemos ver que as distâncias e são iguais, então os módulos duas forças associadas a elas também serão:
Como as duas forças são iguais, e apontam em direções perpendiculares, o módulo da força resultante entre as duas pode ser calculado pelo teorema de Pitágoras:
Apontando exatamente ao longo da diagonal do quadrado (ângulo de ).
Passo 3
Agora vamos pensar na força exercida pela partícula que está na diagonal em relação à partícula verde.
A distância entre as duas pode ser calculada com o teorema de pitágoras:
Então o módulo dessa força é:
Que, conforme o desenho, também aponta exatamente na direção da diagonal do quadrado.
Passo 4
Como agora temos os módulos de três forças que apontam na mesma direção, podemos somar tudo para encontrar a força resultante:
Resposta
A força resultante tem módulo .