Enunciado
Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 27.Exercício - Ex. 1
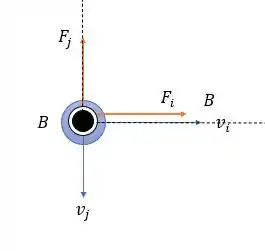
- Uma partícula com a carga igual a se move com velocidade instantânea Qual é a força exercida sobre essa partícula por um campo magnético
Passo 1
Como temos a carga dessa partícula e a velocidade e o campo magnético de forma vetorial então temos que aplicar a força magnética de forma vetorial também e da seguinte forma:
Isso levando em consideração o sinal da carga também (na parte escalar que podemos ignorar o sinal na vetorial não, pois isso influência no sentido da carga). Então a letra nós temos:
Agora lembrando da forma de multiplicação vetorial abaixo:
E a nossa conta tem um que dá e outra multiplicação que dá , então a conta dessa força fica igual a:
Então a direção da força está na direção e tem intensidade igual a .
Viu como a carga da partícula influencia na direção da força? Por isso que a regra da mão esquerda não é válida nessa partícula, e sim o inverso disso.
De forma vetorial dizemos que a carga tem força entrando na folha do papel (-k) nos deixando com a seguinte representação vetorial.
Passo 2
Agora para a letra temos a seguinte conta vetorial para fazer:
Onde temos uma multiplicação que dá e outra multiplicação que dá , então temos uma conta igual a:
Então a força vetorial nessa partícula será:
Como agora o campo magnético está em , nós dizemos que esse vetor sai da folha do papel e a forma vetorial das componentes nessa partícula será:
