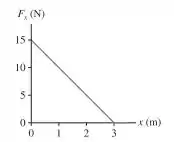
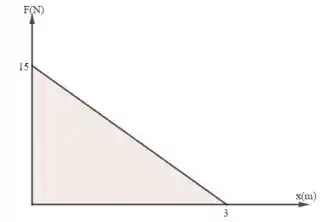
Uma partícula de 500 g que se move ao longo do eixo x experimenta a força representada na FIGURA EX11.15. A velocidade da partícula é de 2,0 m/s em x = 0 m. Qual é sua velocidade em x = 1 m, 2 m e 3 m?
Passo 1
Vamos entender o que está acontecendo. Vamos supor que a partícula está movendo para a direita a força começa atura nela no momento em que ela passa por . Essa força está orientada para a direita. Como a força está no mesmo sentido que a velocidade, a força irá acelerar essa partícula, ou seja, a velocidade da partícula vai ficando cada vez maior...
Porém, pelo gráfico vemos que a intensidade da força vai diminuindo conforme a partícula vai se movimentando... isso só significa que a aceleração que a partícula sofre também vai diminuindo (lembre-se que F = ma, se F diminui, a também diminui).... porém, essa aceleração ainda estará orientada para a direita, de modo que a partícula continua ganhando velocidade até atingir o ponto x = 3.
Passo 2
Agora a questão é... como calculamos a velocidade x = 1, 2 e 3 m? Vamos utilizar o teorema da energia cinética. Tal teorema diz que o trabalho realizado pela força resultante em uma partícula é igual a variação de sua energia cinética. Em linguagem matemática isso se traduz em:
onde: m é a massa da partícula, é a velocidade final e é a velocidade inicial!
Mas como calculamos esse trabalho? Como foi dado o gráfico de o trabalho será igual à área sob o gráfico, ou seja,
Passo 3
- Para , temos:
- Para , temos o mesmíssimo procedimento:
- , por fim, temos:
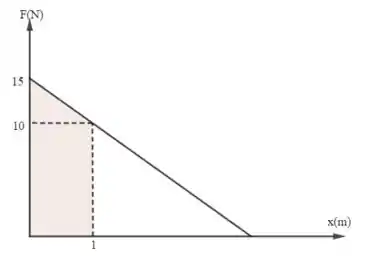
A área hachurada é de um trapézio. Assim,
Agora, vamos aplicar o teorema da energia cinética (a massa vale 0,5 kg e a velocidade inicial 2,0 m/s).
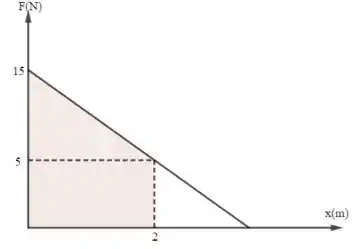
Portanto, aplicando o teorema da energia cinética:
Portanto, aplicando o teorema da energia cinética:
Resposta
7,35 m/s; 9,17 m/s; 9,70 m/s.