59. Um engenheiro esperto projeta uma mola que não satisfaz à lei de Hooke, mas que obedece à lei de força , onde é a posição de equilíbrio da extremidade da mola e é a constante elástica da mola. Por simplicidade, vamos considerar . Com isso, .

a. Qual é a unidade de ?

b. Desenhe o gráfico de versus .

c. Obtenha uma expressão para a energia potencial desta mola distendida ou comprimida.

d. Uma arma de brinquedo funciona com uma mola desse tipo que arremessa uma bola de plástico de . Quanto vale a velocidade de lançamento se o valor da constante elástica da mola for de , nas unidades que você determinou no item a, e se a mola for comprimida em ? Considere que não exista atrito no cano da arma.

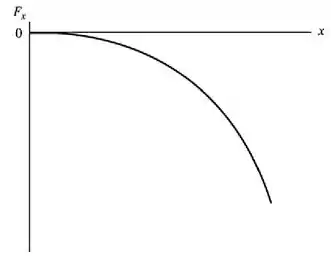
b) Em seguida, vamos plotar o gráfico da força em função da distância .

Para cada valor positivo de que usarmos, o valor de vai sempre ser negativo.

E cada vez que aumentamos esse valor de , a força será ainda menor. De modo que temos o seguinte gráfico exposto na imagem abaixo...

c) Já no caso da expressão da energia potencial da mola... Para se resolver este item, bastar saber que a força elástica é nada mais nada menos do que o negativo da derivada da energia potencial em relação a posição ;

Bom! A partícula sai da posição inicial de equilíbrio para uma posição qualquer. Sendo assim, nosso limite de integração vai de até . E ficamos com...

d) Pra finalizar, temos que achar a velocidade de lançamento da bola.

Bora lá! Pelo que sabemos do enunciado a mola é comprimida e o resultado dessa compressão faz com que a bola seja liberada com uma velocidade tal, que nós queremos saber.

Desse modo, fica fácil de entender que estamos nos deparamos com uma situação no qual energia potencial elástica é convertida em energia cinética.

Assim,

E substituindo os valores que temos... Lembrando que uma vez que a mola foi comprimida em , o valor de vai ser ou ...

Pronto! Obtemos nossa resposta e finalizamos aqui!