Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 5.Problemas - Ex. 117
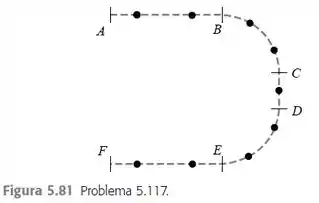
Uma partícula se move sobre uma superfície sem atrito ao longo da trajetória indicada na Figura 5.81. (A figura mostra uma vista de topo sobre a superfície.) A partícula está inicialmente em repouso no ponto A, a seguir ela começa a mover-se até o ponto B à medida que ganha velocidade com uma taxa constante. De B até C a partícula se move ao longo de uma trajetória circular com velocidade constante. A velocidade permanece constante ao longo do trecho retilíneo de C até D. De D até E a partícula se move ao longo de uma trajetória circular, mas agora sua velocidade está diminuindo com uma taxa constante. A velocidade continua a diminuir com uma taxa constante enquanto a partícula se move de E até F; a partícula entra em repouso no ponto F. (Os intervalos de tempo entre os pontos marcados não são iguais.) Para cada ponto marcado por ponto em negrito, desenhe flechas para indicar a velocidade, a aceleração e a força resultante sobre a partícula. Use flechas maiores ou menores para representar os vetores que possuem módulos maiores ou menores.
Passo 1
Em todos os pontos a aceleração terá a mesma orientação da força resultante . Nos pontos a aceleração vai ser a linear, já bem conhecida. Nos pontos entre e a aceleração será centrípeta, pois a trajetória é curva e sua direção é voltada para dentro da trajetória.
No ponto entre , a aceleração é nula .
Passo 2
E quanto a velocidade? Tanto no início quanto no fim da trajetória ela é nula . E vai ser máxima entre os pontos .
A velocidade é orientada em sentido horário, partindo de até chegar em , sempre tangente à curva.
Passo 3
Juntando todas essas informações, os vetores aceleração, força resultante e velocidade no desenho ficam assim:
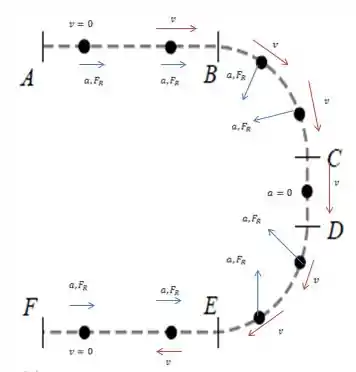
Resposta
