Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 5.Problemas - Ex. 93
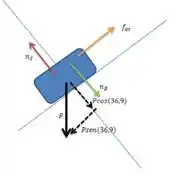
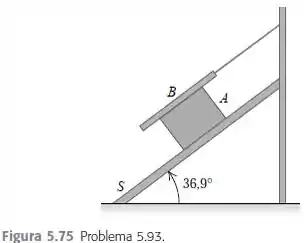
Um bloco , com peso , desliza sobre um plano inclinado S com inclinação de a uma velocidade constante, enquanto a prancha , com peso , está em repouso sobre . A prancha está ligada por uma corda no topo do plano (Figura ).
a) Faça um diagrama de todas as forças que atuam sobre .
b) Se o coeficiente de atrito cinético entre e for igual ao coeficiente de atrito cinético entre e , calcule o seu valor.
Passo 1
Fala galera, tudo bem? Essa questão parece confusa, mas vou ajudar você aqui!
Letra a)
O problema começa pedindo um diagrama com todas as forças que atuam sobre . As forças que a gente conhece são: normal, peso, atrito e tensão, certo? No caso do bloco a única que não se aplica é a tensão, pois o bloco não está preso por nenhum fio. E como eu sei que tem atrito? Ora bolas, vamos imaginar se não tivesse! Se não tivesse atrito do bloco com o plano inclinado ele iria deslizar por causa da força peso (que seeeeempre existe, ok?). Então, se o bloco está com velocidade constante, então temos um equilíbrio de forças na direção do movimento e consequentemente, temos uma força atrito.
Com isso, vamos construir esse diagrama.
Sobre o bloco estão agindo as seguintes forças:
- A força peso , vertical para baixo, perpendicular ao chão. Nesse movimento podemos decompor essa força em duas componentes: vertical e horizontal em relação ao bloco;
- Temos as forças de atrito que são paralelas à superfície , contrárias ao movimento. Como o bloco desliza da direita para a esquerda, a força de atrito estará direcionada para a direita;
- E por fim temos a força normal. Aqui temos duas: a normal que a superfície faz no bloco empurrando ele para cima e a outra é a força que é a força que a prancha faz empurrando o bloco para baixo.
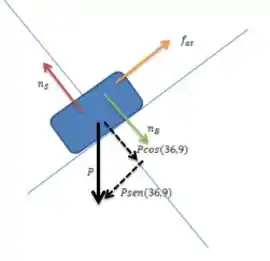
Juntando todas essas informações, o diagrama de forças fica assim:
Passo 2
Letra b)
Se o bloco não está se movendo na direção vertical, logo o somatório das forças deve ser igual a zero, certo? Vamos considerar que para cima é positivo e para baixo é negativo:
Você concorda comigo que a força que a prancha B faz empurrando o bloco A é o componente vertical do peso da prancha B? Já falamos que a prancha B tem peso igual a :
O módulo da força peso do bloco A é . Assim na vertical temos:
Assim depois de termos calculado a força normal do bloco vamos conseguir determinar o coeficiente de atrito que o problema pede.
Passo 3
A força de atrito total vai ser a soma da força de atrito entre o bloco e a superfície e da prancha e o bloco. Assim teremos:
Substituindo os valores que já conhecemos de e :
Passo 4
E para o sistema se mover com velocidade constante essa força de atrito total deve contrabalançar a componente horizontal do peso :
Resposta
