Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 3.Problemas - Ex. 60
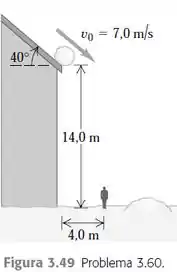
Um Uma bola de neve rola do telhado de um celeiro que possui uma inclinação para baixo igual a (Figura ). A extremidade do telhado está situada a acima do solo e a bola de neve possui velocidade de quando ela abandona o telhado. Despreze a resistência do ar.
a) A que distância do celeiro a bola de neve atingirá o solo caso não colida com nada durante sua queda?
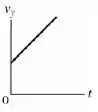
b) Faça diagramas, yt, e para o movimento da parte
Passo 1
Queremos saber o alcance dele. Começando pela equação de movimento vertical:
Aqui temos as seguintes condições iniciais:
Vamos admitir que o eixo positivo seja para baixo. Substituindo os valores teremos uma equação de segunda ordem para o tempo:
Usando a fórmula de bháscara teremos as raízes dessa equação:
Jogando tudo isso na calculadora, vamos encontrar duas raízes, mas só a positiva nos interessa, né? Então teremos:
Então nesse instante de tempo a bola de neve chega ao chão. Daí que entra o movimento na horizontal. Para determinar o alcance, utilizamos esse valor de tempo e a velocidade (que é constante) inicial . Daí com a fórmula conhecida como “deus vê tudo”:
Passo 2
As equações para o movimento vertical são:
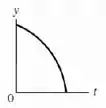
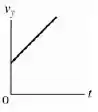
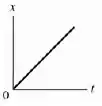
No movimento horizontal não temos aceleração, então o gráfico da velocidade vai ser uma reta horizontal em . Já para a posição a equação é:
Vai ser uma reta crescente com seu ponto inicial na origem. Os gráficos ficam assim:
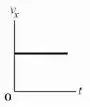
Passo 3
Vamos primeiro achar quanto tempo a bola leva para percorrer a distância de e depois usar essa informação para achar a posição vertical dela, ok?
Do movimento horizontal:
Agora do movimento vertical:
Bom, se o homem tem de altura, a bola vai passar a uma distância de acima dele, sem atingi-lo.
Resposta
