Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 5.Problemas - Ex. 111
No rotor de um parque de diversões, as pessoas ficam em pé contra uma parede interna de um cilindro oco vertical com raio de . O cilindro começa a girar e quando ele atinge uma rotação de , o piso onde as pessoas se apoiam desce cerca de As pessoas ficam presas contra a parede.
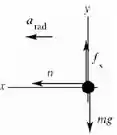
a) Faça um diagrama de forças para um passageiro, depois que o piso abaixou.
b) Qual deve ser o coeficiente de atrito estático mínimo necessário para que o passageiro não escorregue para baixo na nova posição do piso?
c) A sua resposta do item (b) depende da massa do passageiro? (Nota: Quando a viagem termina, o cilindro volta lentamente para o repouso. Quando ele diminui de velocidade as pessoas escorregam para baixo até o piso.)
Passo 1
Eaee, belezinha?? Bom... o enunciado nos diz que em um rotor de um parque de diversões, as pessoas ficam em pé contra uma parede interna de um cilindro oco vertical com raio de .
O cilindro começa a girar e quando ele atinge uma rotação de , o piso onde as pessoas se apoiam desce cerca de
Com essa força centrípeta, as pessoas ficam presas contra a parede.
Queremos fazer um diagrama de corpo livre para um passageiro depois que o piso baixou.
Para isso, temos que analisar as forças que estão atuando no passageiro... os módulos e sentidos.
Também queremos calcular o coeficiente de atrito estático mínimo necessário para que o passageiro não escorregue para baixo na nova posição do piso.
Para isso, temos que saber que a força de atrito é:
Onde é a força normal.
Também devemos saber que a força centrípeta é dada por:
Onde é a velocidade e é o raio.
Passo 2
O passageiro se move em torno de um círculo horizontal e sua aceleração é a aceleração centrípeta direcionada para o centro da circunferência.
Quando do chão é removido, o passageiro é sustentado pela força de atrito estático exercido sobre ele pela parede do brinquedo. O diagrama de forças é o seguinte:
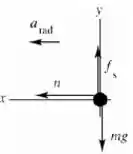
A força de atrito estático é vertical para cima, pois está em oposição ao movimento do corpo pela força gravitacional (que é orientada na vertical para baixo).
A força normal aponta para o centro da trajetória, assim como a aceleração centrípeta (radial).
Passo 3
Vamos aplicar a segunda lei na direção vertical e horizontal e combinar as equações para determinar o coeficiente de atrito estático .
Na vertical vamos ter:
Na horizontal temos a expressão para a normal:
Combinando as duas equações teremos:
Agora é só substituir os valores dados:
Passo 4
Percebemos que esse valor independe da massa. Apenas depende da velocidade do cilindro.
Quanto menor for o coeficiente de atrito, mais rápido o cilindro deve girar para que as pessoas fiquem suspensas.
Resposta
