Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 11.Exercícios e Problemas - Ex. 36
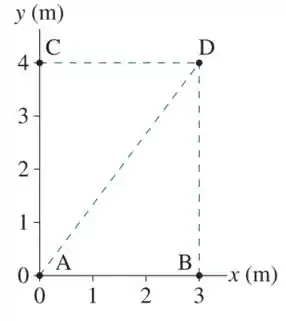
Uma partícula move-se de A para D, como ilustrado na FIGURA P11.36, enquanto experimenta a força . Que trabalho realiza esta força se a partícula segue a trajetória
e
?
Trata-se ou não de uma força conservativa? Explique.
Passo 1
O trabalho, de forma vetorial, é calculado por:
Onde é a distância, então tipo para a letra a distância pode ser vista como:
Portanto o trabalho para a letra será:
Aplicando os valores teremos:
Como multiplicação escalar somente se faz com coeficientes no mesmo eixo ou seja e ), então:
Passo 2
Já para o caminho teremos:
Logo o trabalho nesse caminho será:
Fazendo a multiplicação escalar:
Passo 3
E para o caminho nós temos que decompor o eixo nos três eixos o que nos dá:
O que é a mesma coisa que no passo 1.
Na real não importa o caminho que a partícula tome, desde que ela saia de e chegue em o trabalho sempre será de .