Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 6.1 - Ex. 51
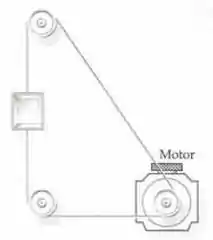
Você deve instalar um pequeno elevador de serviço de alimentação em um refeitório universitário. O elevador está conectado por um sistema de polias a um motor, como mostrado na figura abaixo. O motor ergue e abaixa o elevador. A massado elevador é de 35 kg. Em operação, ele se move com uma rapidez e 0,35 m/s para cima, sem acelerar (exceto no breve período inicial, imediatamente após ligado o motor, que podemos desconsiderar). Os motores elétricos têm, tipicamente, uma eficiência de 78 por cento. Se você compra um motor com uma eficiência de 78 por cento, qual deve ser a potência mínima desse motor? Suponha as polias sem atrito.
Passo 1
Olá! Tá bem? Então, temos um elevador que precisa levantar com velocidade constante a massa de .
Aí ele pergunta para gente a potência que o motor desse elevador precisa ter, considerando que o motor tem de eficiência.
Olha, podemos pensar em potência como o produto escalar entre o vetor força necessário para levantar a massa e a velocidade que essa massa vai ter. Fica assim:
Só que ele diz que a rapidez do elevador é . Se a gente considerar que essa é a rapidez com que o elevador sobe, o vetor velocidade fica:
Esse representa que a velocidade está voltada para cima apenas (sentido positivo de )
Passo 2
Mas quem vai ser ? Cara, percebe que o o esforço que o elevador vai fazer vai ser para levantar a massa? Então a gente tem essa situação:
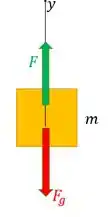
Para levantar o elevador, está para cima. Como a velocidade dessa massa é constante, temos que . Então se a gente aplicar a segunda lei de Newton para esse caso, fica assim:
Como :
Colocando isso na forma vetorial, já que está o sentido positivo de :
Substituindo os valores:
Passo 3
Aí a gente pode calcular o produto escalar para achar a potência necessária para levantar a massa:
Como só temos componentes em cada vetor, o produto escalar vai ser somente o produto entre esses dois valores mesmo:
Passo 4
Só que esse é o valor de potência que a gente precisa ter na situação real.
Mas queremos saber a potência que o motor precisa ter para dar essa potência na situação real.
Já que a eficiência do motor é de 78%, a potência disponível de fato para levantar a massa vai ser da potência do motor:
Isolamos :
Agora a gente substitui os valores: