Uma partícula pontual de massa está se movendo com rapidez constante ao longo de uma linha reta que passa pelo ponto . O que você pode afirmar sobre o momento angular da partícula em relação ao ponto ? (a) Sua magnitude é . (b) Sua magnitude é zero. (c) Sua magnitude muda de sinal quando a partícula passa pelo ponto . (d) Sua magnitude aumenta conforme a partícula se aproxima do ponto .
Passo 1
Vamos fazer um esquema da situação:
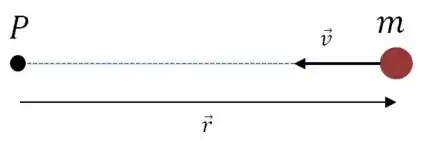
A expressão para o momento angular da massa em relação ao ponto é a seguinte:
Onde é o vetor posição que liga até a massa , e é o momento linear da massa :
E então:
Passo 2
Dando uma olhada na figura, os vetores e são paralelos e, portanto, o produto vetorial entre eles é zero.
Podemos verificar isso definindo um vetor unitário que aponta para a direita na direção representada no desenho:
E podemos escrever esse produto vetorial como um determinante:
E então a alternativa correta é a (b).
Resposta
Letra (b).