Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 11.Exercícios e Problemas - Ex. 14
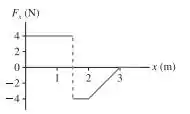
A FIGURA EX11.14 é o gráfico força versus posição de uma partícula que se move ao longo do eixo x. Determine o trabalho feito sobre a partícula durante cada um dos intervalos 0-1 m, 1-2 m e 2-3 m.
Passo 1
Foi dado o gráfico da força versus o deslocamento da partícula .
Pela definição de trabalho, sabemos que:
Mas, geometricamente, o que representa a integral acima? Lembre-se que toda integral representa a área sob o gráfico da função limitada pelas retas e . Veja a figura abaixo.
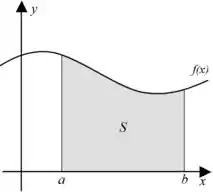
Assim, calcular a integral é equivalente a calcular a área sob o gráfico .
Não se esqueça de uma coisinha... : quando o gráfico estiver acima do eixo x essa área vai ser positiva, e quando o gráfico estiver abaixo do eixo x essa área vai ser negativa, ok? Vamos usar isso no exercício.
Passo 2
Vamos calcular o trabalho de cada trecho a partir da área sob o gráfico.
- De até , temos o seguinte esquema:
- De até m temos a seguinte situação
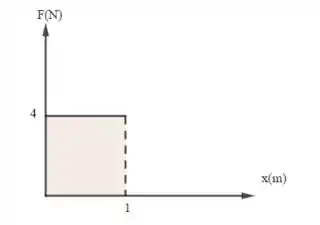
A nossa figura é um retângulo de altura 4 e base 1. Assim, a área (ou seja, o trabalho), será:
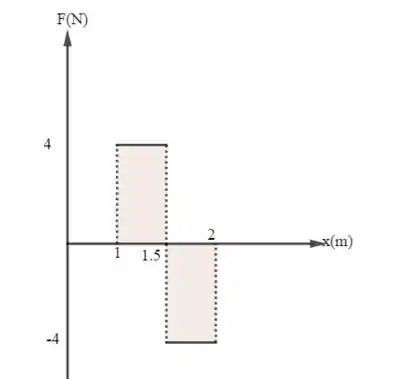
Lembrando que a área abaixo do eixo x é negativa, temos:
De x = 2 até x = 3 m, temos o seguinte esquema
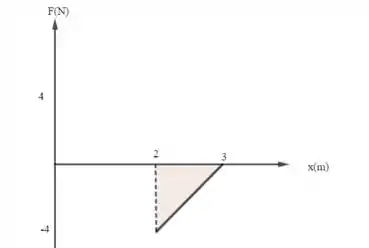
O trabalho será igual a área do triângulo acima:
Resposta
4J, 0, -2 J.