Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Tipler - Vol 2- Ed: 6º - Capítulo 21.1 - Ex. 33

Uma partícula puntiforme que tem uma carga de - 1,0   μ C está localizada na origem; uma segunda partícula puntiforme que tem carga de 2,0   μ C está localizada em x = 0 , y = 0,10   m ; e uma terceira partícula puntiforme que tem uma carga de 4,0   μ C está localizada em x = 0,20   m e y = 0 . Determine a força elétrica em cada uma das três cargas puntiformes.

Passo 1

O esquema a seguir exemplifica o que o enunciado disse:

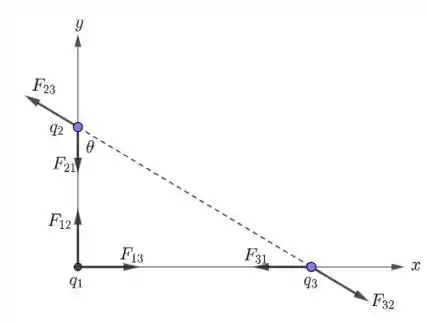
Da figura, temos que

d 23 = d 2 2 + d 3 2 = 0,1 2 + 0,2 2 = 0,22   m

cos ⁡ θ = d 2 0,22 = 0,45 ⟹ θ = 63,43 °

Vamos calcular vetorialmente cada força:

F → 12 = k q 1 q 2 d 1 2 y ^ = 9 × 10 9 1 × 10 - 6 2 × 10 - 6 0,1 2 y ^ = 1,8   N   y ^

F → 21 = - F → 12 = - 1,8   N   y ^

F → 13 = k q 1 q 3 d 3 2 x ^ = 9 × 10 9 1 × 10 - 6 4 × 10 - 6 0,2 2 = 0,9   N   x ^

F → 31 = - F → 13 = - 0,9   N   x ^

F → 32 = k q 2 q 3 d 23 2 sen ⁡ θ   x ^ - cos ⁡ θ   y ^ = 9 × 10 9 2 × 10 - 6 4 × 10 - 6 0,22 2 0,894   x ^ - 0,449   y ^ F → 32 = 1,29   N   x ^ + - 0,64   N   y ^

F → 23 = - F → 32 = - 1,29   N   x ^ + 0,64   N   y ^

Passo 2

Assim, podemos calcular a força resultante em cada partícula:

  • Partícula 1 :

    • F → 1 = F → 12 + F → 13 = 0,9   N   x ^ + 1,8   N   y ^

    F 1 = 0,9 2 + 1,8 2 = 2,01   N

  • Partícula 2:

    • F → 2 = F → 21 + F → 23 = 1,29   N   x ^ + - 1,16   N   y ^

    F 2 = 1,29 2 + 1,16 2 = 1,73   N

  • Partícula 3:

F → 3 = F → 31 + F → 32 = 0,39   N   x ^ + - 0,64   N   y ^

F 3 = 0,39 2 + 0,64 2 = 0,75   N

Resposta

F → 1 = 0,9   N   x ^ + 1,8   N   y ^

F → 2 = 1,29   N   x ^ + - 1,16   N   y ^

F → 3 = 0,39   N   x ^ + - 0,64   N   y ^

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A Fig. 21-44 mostra uma barra longa, não condutora, de massa desprezível, de comprimento L , articulada no centro e equilibrada por um bloco de peso P situado a uma distância x da extremidade esquerda
Qual seria o módulo da força eletrostática entre duas cargas pontuais de 1,00C separadas por uma distância de (a)1,00 m e (b) 1,00k m se essas cargas pontuais pudessem existir (o que não é verdade) e
Sabemos que a carga negativa do elétron e a carga positiva do próton têm o mesmo valor absoluto. Suponha, porém, que houvesse uma diferença de0,00010 % entre as duas cargas. Nesse caso, qual seria a f
Na Fig. 21-42, seis partículas carregadas cercam a partícula 7 a uma distância de d=1,0c m ou 2 d , como mostra a figura. As cargas são q 1=+ 2 e , q 2=+ 4 e , q 3=+ e , q 4=+ 4 e , q 5=+ 2 e , q 6=+
Uma carga de 6,0μ C é dividida em duas partes, que são mantidas a uma distância de 3,00m m . Qual é o maior valor possível da força eletrostática entre as duas partes?