Uma partícula viaja em linha reta com a rapidez constante de 25,0 m/s. Repentinamente, uma força de 15,0 N age sobre ela, levando-a ao repouso em uma distância de 62,5 m. (a) Qual é a orientação da força? (b) Determine o tempo que a partícula leva para atingir o repouso. (c) Qual é a massa da partícula?
Passo 1
a) Oi pessoal, tudo bem? Vamos analisar este probleminha.
O enunciado nos diz que a partícula está em movimento e uma força age sobre ela levando-a ao repouso. Qual é a orientação da força?
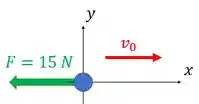
Para que isso aconteça, a força deve ter orientação oposta ao movimento, pois essa força produz uma aceleração sobre a partícula que vai reduzir a velocidade da partícula. E ela reduz a velocidade exatamente por ter sentido oposto ao da velocidade.
Essa orientação oposta entre força e velocidade da partícula é mostrada na figura.
Passo 2
b) A gente quer determinar o tempo que a partícula leva para atingir o repouso, o problema diz que a velocidade da partícula é constante no primeiro momento.
Mas agora como tem uma força agindo sobre ela ela vai passar a ter a aceleração referente a força aplicada, por isso podemos usar a definição de aceleração:
Como o velocidade final é zero, temos:
Isolando :
Temos a velocidade inicial, mas não temos a aceleração . Falta achar esse cara!
Passo 3
Para achar aceleração sem saber o tempo, mas sabendo o deslocamento e a velocidade final e inicial, podemos usar essa equação aqui que vale quando temos aceleração constante:
A gente chama essa bonita de equação de Torriceli. A velocidade final é zero:
Isolando :
Agora temos uma expressão para .E podemos substituir na equação de tempo:
Dando aquela arrumadinha:
Só relembrando, peo enunciado temos, e , substituindo:
Passo 4
c) Pra encerrar, só falta encontrar a massa da partícula, podemos aplicar a segunda lei de Newton:
Só temos uma força e ela só atua em , no sentido contrário da velocidade, então colocamos um sinal negativo:
Isolando a massa:
Não temos a aceleração , mas no Passo 3 vimos que:
Substituindo:
Arrumando:
Agora só precisamos substituir os valores, lembrando que :
Aweeee!