Usa-se ar comprimido para disparar uma bola de verticalmente para cima ao longo de um tubo de de altura. O ar exerce uma força para cima de sobre a bola enquanto ela se encontra dentro do tubo. Que altura acima da boca do tubo a bola atingirá?
Passo 1
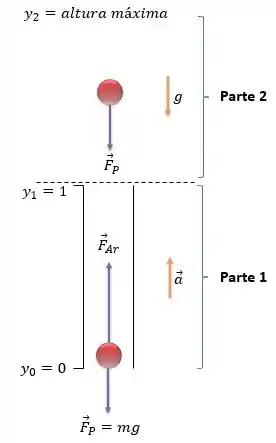
Primeiro de tudo vamos representar essa situação e as forças que atuam sobre a bola, beleza?
Esse é um problema dividido em duas partes:
Parte 1: Enquanto a bola está dentro do tubo ela está sob a ação de duas forças, a força do ar comprimido e a força peso e possui uma aceleração positiva, para cima.
Parte 2: Após a bola sair do tubo, não há mais ação da força do ar comprimido. Assim, a bola está sujeita apenas a aceleração da gravidade, para baixo, de modo que ela atinge um pico e em seguida sofrerá a queda livre.
Passo 2
Vamos olhar primeiro para a Parte 1:
Podemos utilizar a segunda lei de Newton para encontrar a aceleração:
Nesse momento a força resultante é:
A massa e a força que o ar comprimido faz foram fornecidos na questão e a aceleração da gravidade é um valor conhecido:
Obs.: A massa precisa estar em para a força no final sair em Newton, show?
Então:
Retornando à segunda lei de Newton:
Passo 3
Agora que já conhecemos a aceleração podemos calcular qual a velocidade final na Parte 1, ou seja, a velocidade com a qual a bola chega à boca do tubo.
Vamos utilizar a equação de Torricelli:
Como a bola parte do repouso:
A distância que a bola percorre na Parte 1 é o comprimento do tubo:
Então:
Passo 4
Agora, vamos olhar para a Parte 2
Para sabermos qual a altura a bola atingirá acima da boca do tubo precisamos saber qual a distância percorrida, , na Parte 2.
Vamos utilizar novamente a equação de Torricelli:
A velocidade inicial da Parte 2 é a velocidade final, , da Parte 1.
A velocidade final da Parte 2 é zero, , porque a bola atinge a altura máxima, quando a velocidade é zero e depois começa a sofrer queda livre.
E a aceleração na Parte 2 é a própria aceleração da gravidade:
Então:
Logo, a bola atingirá acima da boca do tubo.
Resposta
A bola atingirá acima da boca do tubo.